题目内容
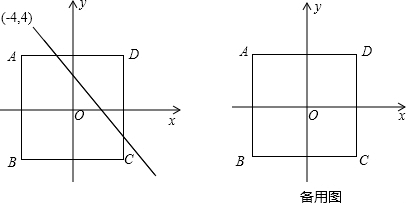
3.对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小的长度为G1、G2的“密距”,当线段PQ的长度取最大值时,我们称这个最大的长度为图形G1,G2的“疏距”.请你在学习、理解上述定义的基础上,解决下面的问题:如图,在平面直角坐标系xOy中,点A的坐标为(-4,4),正方形ABCD的对称中心点O.
(1)线段AB和CD的“密距”是8,“疏距”是8$\sqrt{2}$.
(2)设直线y=-$\frac{3}{4}$x+b(b>0)与x轴、y轴分别交于点E、F,若线段EF与正方形ABCD的“密距”是1,求它们的“疏距”;
(3)在同一平面直角坐标系xOy中有一个四边形KLMN,将正方形ABCD绕点O旋转一周,在旋转过程中,它与四边形KLMN的“疏距”的最大值为4$\sqrt{2}$+2,在旋转过程中,求它与四边形KLMN的“密距”的取值范围.
分析 (1)线段AB与CD的“密距”是AD或BC的长度;
(2)先求得直线OA的解析式,可知直线EF与OA垂直,故点C到直线EF的距离为“疏距”;
(3)当O、K、D在一条直线上时,密距有最小值,当OK⊥AD时,密距有最大值.
解答  解:(1)如图1所示:
解:(1)如图1所示:
由垂线的性质可知:线段AB与CD的“密距”是AD或BC的长度,
故“密距”是8.
在Rt△ADC中,由勾股定理得:
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=8$\sqrt{2}$,
“疏距”是8$\sqrt{2}$;
故答案为:8;8$\sqrt{2}$;
(2)如图2所示:
设直线OD的解析式为y=kx,
将x=4,y=4代入函数的解析式得4=4k,
解得:k=1,
∵直线EF的解析式为y=-$\frac{3}{4}$x+b,
∴直线OB和EF相互垂直.
∵EF与矩形ABCD的“密距”是1,
∴点D到EF的距离最长=8$\sqrt{2}$+1,
即“疏距”=8$\sqrt{2}$+1;
(3)①当K在BD上时,
如图3所示: 正方形ABCD与四边形KLMN的“疏距”为KB=4$\sqrt{2}$+2,
正方形ABCD与四边形KLMN的“疏距”为KB=4$\sqrt{2}$+2,
∴KD=BD-BK=8$\sqrt{2}$-(4$\sqrt{2}$+2)=4$\sqrt{2}$-2,
故最大密距=4$\sqrt{2}$-2;
②当OK⊥AD时,
如图4所示:
正方形ABCD与四边形KLMN的“密距”有最小值,
∵正方形的边长为8,
∴O到AD的距离为4, 又由①可知OK=OD-KD=4$\sqrt{2}$-(4$\sqrt{2}$-2)=2,
又由①可知OK=OD-KD=4$\sqrt{2}$-(4$\sqrt{2}$-2)=2,
所以密距的最小值=4-OK=4-2=2,
故密距的范围为:2≤密距≤4$\sqrt{2}$-2.
点评 本题是一次函数综合题目,考查了一次函数解析式的求法、勾股定理、两点间的距离、点到直线的距离等知识;本题综合性强,根据题意画出图形是解决问题的关键.题目较为新颖,难度适中.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,由三个小立方块搭成的俯视图是( )
如图,由三个小立方块搭成的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
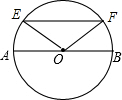 如图,在⊙O中,弦EF∥直径AB,如果$\widehat{AE}$的度数为50°,那么$\widehat{BF}$的度数为50°,∠BOF=50°.
如图,在⊙O中,弦EF∥直径AB,如果$\widehat{AE}$的度数为50°,那么$\widehat{BF}$的度数为50°,∠BOF=50°. 作出图中三角形先向右向右平移5格,再顺时针旋转60°的图案.
作出图中三角形先向右向右平移5格,再顺时针旋转60°的图案.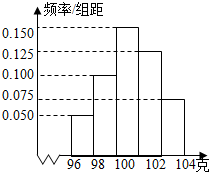 如图是抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
如图是抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )