Question

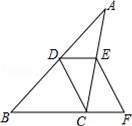
如图，在△ABC中，D、E分别是边AB、AC的中点，延长BC至点F，使得CF=BC，连结CD、DE、EF．

（1）求证：四边形CDEF是平行四边形．

（2）若四边形CDEF的面积为8，则△ABC的面积为　8　．

Answer 1

【考点】平行四边形的判定与性质．

【分析】（1）欲证明四边形CDEF是平行四边形，只需推知DE∥CF，DE=CF；

（2）在四边形CDEF与△ABC中，CF=BC，且它们的高相等．

【解答】（1）证明：∵如图，在△ABC中，D、E分别是边AB、AC的中点，

∴DE∥BC且DE=BC．

又∵CF=BC，

∴DE=CF，

∴四边形CDEF是平行四边形．

（2）解：∵DE∥BC，

∴四边形CDEF与△ABC的高相等，设为h，

又∵CF=BC，

∴S_△ABC=BC•h=CF•h=8，

故答案是：8．

【点评】本题考查了平行四边形的判定与性质．平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．