题目内容
如图,O是矩形ABCD的对称中心,M是AD的中点.若BC=8,OB=5,则OM的长为( )


A.1 B.2 C.3 D.4
C【考点】矩形的性质.
【分析】先由矩形的性质得出AB=CD,根据勾股定理求出AB,再求出OM是△ACD的中位线,即可得出OM的长.
【解答】解:∵四边形ABCD是矩形,
∴AB=CD,OA=
 AC,OB=
AC,OB=
 BD,AC=BD,
BD,AC=BD,
∴AC=BD=2OB=10,
∴AB=
 =6,
=6,
∴AB=6,
∵O是矩形ABCD的对称中心,M是AD的中点,
∴OM是△ACD的中位线,
∴OM=
 CD=3,
CD=3,
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 B.
B.
 C.
C.
 D.
D.


 BC,连结CD、DE、EF.
BC,连结CD、DE、EF.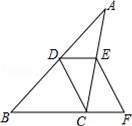

 的零点个数为( )
的零点个数为( ) B.
B. C.
C. D.
D.