题目内容
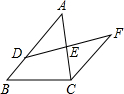如图，D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，若BD=2cm，CF=4cm，则AB等于（ ）cm．| A、2cm | B、4cm |
| C、6cm | D、8cm |
考点：全等三角形的判定与性质
专题：
分析：由FC与AB平行，利用两直线平行得到两对内错角相等，再由DE=FE，利用AAS得到三角形ADE与三角形CFE全等，利用全等三角形的对应边相等得到AD=CF，由AB=AD+DB，等量代换即可求出AB的长．
解答：解：∵FC∥AB，
∴∠A=∠ACF，∠ADF=∠F，
在△ADE和△CFE中，
，
∴△ADE≌△CFE（AAS），
∴CF=AD，
则AB=AD+DB=CF+BD=2+4=6cm．
故选C．
∴∠A=∠ACF，∠ADF=∠F，
在△ADE和△CFE中，
|
∴△ADE≌△CFE（AAS），
∴CF=AD，
则AB=AD+DB=CF+BD=2+4=6cm．
故选C．
点评：此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
如图，正方形ABCD的边长为2，P为正方形ABCD内一点，且△PBC为等腰三角形，则△CDP的面积为
如图所示，两平面镜OM、ON的夹角为∠θ，入射光线AB沿着与镜面ON平行的方向照射到镜面OM上，经过两次反射后的反射光线CD平行于镜面OM，求∠θ的度数．