题目内容
长为10, 7, 5, 3的四根木条,选其中三根首尾顺次相连接组成三角形,选法有( )
A. 1种 B. 2种 C. 3种 D. 4种
练习册系列答案
相关题目
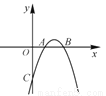
已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.
已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
查看答案已知关于x的方程x2+ax+a-2=0.
(1)若该方程的一个根为1,求a的值及该方程的另一个根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案用适当的方法解下列方程.
①(2x+3)2﹣16=0;
②2x2=3(2x+1).
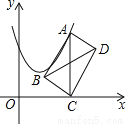
查看答案如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为____.
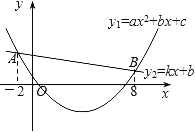
已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+b(k≠0)的图象相交于点A(﹣2,4),B(8,2)(如图所示),则能使y1>y2成立的x的取值范围是 .
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


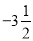 的相反数、倒数、绝对值的和是______________。
的相反数、倒数、绝对值的和是______________。
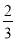
 ,1.5,﹣3.
,1.5,﹣3.
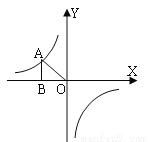
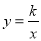 图象上一点,AB垂直x轴于B点.若S△AOB=5,则k的值为_________.
图象上一点,AB垂直x轴于B点.若S△AOB=5,则k的值为_________.