题目内容
2.计算:($-\frac{1}{2}$)-1+4cos60°-|-3|+$\sqrt{9}$.分析 根据实数的运算顺序,首先计算乘方、开方、乘法,然后从左向右依次计算,求出算式($-\frac{1}{2}$)-1+4cos60°-|-3|+$\sqrt{9}$的值是多少即可.
解答 解:($-\frac{1}{2}$)-1+4cos60°-|-3|+$\sqrt{9}$
=-2+4×$\frac{1}{2}$-3+3
=-2+2-3+3
=0
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.正确化简各数是解题关键.

练习册系列答案
相关题目
12.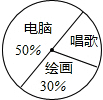 如图是八年级(2)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数为( )
如图是八年级(2)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数为( )
 如图是八年级(2)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数为( )
如图是八年级(2)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数为( )| A. | 36° | B. | 72° | C. | 108° | D. | 180° |
17.某工程队准备修建一条长1200米的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快20%,结果提前两天完成任务,若设原计划每天修建道路x米,则根据题意可列方程为( )
| A. | $\frac{1200}{x}$-$\frac{1200}{(1+20%)x}$=2 | B. | $\frac{1200}{(1-20%)x}$-$\frac{1200}{x}$=2 | ||
| C. | $\frac{1200}{(1+20%)x}$-$\frac{1200}{x}$=2 | D. | $\frac{1200}{x}$-$\frac{1200}{(1-20%)x}$=2 |
7.若$\sqrt{(x-1)^{2}}$=1-x,则( )
| A. | x<1 | B. | x≤1 | C. | x>1 | D. | x≥1 |
14.如果把分式$\frac{xy}{x+y}$中的x和y都扩大为原来的2倍,那么分式的值( )
| A. | 扩大为原来的4倍 | B. | 扩大为原来的2倍 | C. | 不变 | D. | 缩小为原来的$\frac{1}{2}$ |
11.一组数据2,0,-2,1,3的中位数是( )
| A. | -1 | B. | -2 | C. | 1 | D. | 1.5 |
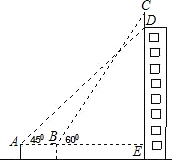 如图某幢大楼顶部有一广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一直线(∠AEC=90°)上,若BE=15米,求这块广告牌的CD.(取 $\sqrt{3}$=1.73,计算结果保留整数)
如图某幢大楼顶部有一广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一直线(∠AEC=90°)上,若BE=15米,求这块广告牌的CD.(取 $\sqrt{3}$=1.73,计算结果保留整数)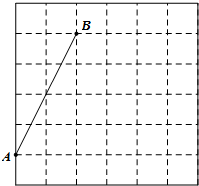 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.