题目内容
8.如果点P(x2-4,y+1)是坐标原点,则2x+y=1或-3.分析 由点P(x2-4,y+1)是坐标原点,可得x2-4=0,y+1=0,继而求得答案.
解答 解:∵点P(x2-4,y+1)是坐标原点,
∴x2-4=0,y+1=0,
解得:x=±2,y=-1,
∴2x+y=1或-3.
故答案为:1或-3.
点评 此题考查了点的坐标特征.注意坐标原点是(0,0).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.化简$\sqrt{5×(-2)^{2}}$,结果是 ( )
| A. | 2$\sqrt{5}$ | B. | -2$\sqrt{5}$ | C. | -10 | D. | 10 |
17.下列等式中不一定成立的是( )
| A. | $\frac{y}{x}=\frac{xy}{x^2}$ | B. | $\frac{y}{x}=\frac{πy}{πx}$ | C. | $\frac{y}{x}=\frac{yz}{xz}$ | D. | $\frac{y}{x}=\frac{{y({{x^2}+2})}}{{x({{x^2}+2})}}$ |
18.|a|=a,则有理数a为( )
| A. | 正数 | B. | 负数 | C. | 正数和0 | D. | 负数和0 |
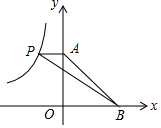 如图,反比例函数y=$\frac{k}{x}$的图象上有点P,PA⊥y轴于点A,点B在x轴的正半轴上,若△PAB的面积为6,则反比例函数的解析式是y=-$\frac{12}{x}$.
如图,反比例函数y=$\frac{k}{x}$的图象上有点P,PA⊥y轴于点A,点B在x轴的正半轴上,若△PAB的面积为6,则反比例函数的解析式是y=-$\frac{12}{x}$.
 根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是(a+b)(a-b)=a2-b2.
根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是(a+b)(a-b)=a2-b2.