题目内容
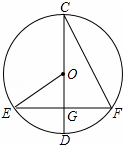 如图,⊙O的直径CD⊥EF,∠OEG=28°,则∠DCF=
如图,⊙O的直径CD⊥EF,∠OEG=28°,则∠DCF=考点:圆周角定理,垂径定理
专题:
分析:先根据垂径定理得出
=
,故可得出∠DCF=
∠EOG,再由三角形内角和定理求出∠EOD的度数,进而可得出结论.
 |
| DE |
 |
| DF |
| 1 |
| 2 |
解答:解:∵⊙O的直径CD⊥EF,
∴
=
,
∴∠DCF=
∠EOG,
∵∠OEG=28°,
∴∠EOG=90°-28°=62°,
∴∠DCF=
∠EOG=
×62°=31°.
故答案为:31°.
∴
 |
| DE |
 |
| DF |
∴∠DCF=
| 1 |
| 2 |
∵∠OEG=28°,
∴∠EOG=90°-28°=62°,
∴∠DCF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:31°.
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,正方形ABCD的边长为4,点M在边DC上,N是M关于对角线AC的对称点,若DM=1,则说sin∠ADN=
如图,正方形ABCD的边长为4,点M在边DC上,N是M关于对角线AC的对称点,若DM=1,则说sin∠ADN= 如图,矩形ABCD中,AB=2,AD=
如图,矩形ABCD中,AB=2,AD= 如图,在Rt△ABC中,∠CAB=30°,∠C=90°.AD=
如图,在Rt△ABC中,∠CAB=30°,∠C=90°.AD= 如图,?OABC中顶点A在x轴负半轴上,B、C在第二象限,对角线交于点D,若C、D两点在反比例函
如图,?OABC中顶点A在x轴负半轴上,B、C在第二象限,对角线交于点D,若C、D两点在反比例函