题目内容
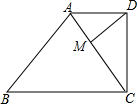如图，已知梯形ABCD中，AD∥BC，∠ACD=∠B，过点D作DM∥AB交AC于点M．（1）写出图中所有相似的三角形，要求将彼此相似的三角形之间用“∽”连接，且对应点写在对应的位置上；
（2）求证：MD•BC=AC•DC．
考点：相似三角形的判定与性质
专题：
分析：（1）根据已知条件结合图形，运用相似三角形的判定定理，即可解决问题．
（2）运用相似三角形的性质，列出比例式，即可解决问题．
（2）运用相似三角形的性质，列出比例式，即可解决问题．
解答：解：（1）∵AD∥BC，
∴∠DAM=∠BCA；
∵DM∥AB，
∴∠AMD=∠BAC，
∴△DAM∽△BCA；
∴∠ADM=∠B，而∠ACD=∠B，
∴∠ADM=∠ACD，而∠DAM=∠CAD，
∴△DAM∽△CAD，
综上所述，图中所有相似的三角形为：
△DAM∽△BCA，△DAM∽△CAD，△BCA∽△CAD．
（2）∵△CAD∽△BCA，
∴
=
；
∵△DAM∽△CAD，
∴
=
，
∴
=
，
∴MD•BC=AC•DC．
解：（1）∵AD∥BC，∴∠DAM=∠BCA；
∵DM∥AB，
∴∠AMD=∠BAC，
∴△DAM∽△BCA；
∴∠ADM=∠B，而∠ACD=∠B，
∴∠ADM=∠ACD，而∠DAM=∠CAD，
∴△DAM∽△CAD，
综上所述，图中所有相似的三角形为：
△DAM∽△BCA，△DAM∽△CAD，△BCA∽△CAD．
（2）∵△CAD∽△BCA，
∴
| AC |
| BC |
| AD |
| AC |
∵△DAM∽△CAD，
∴
| AD |
| AC |
| MD |
| DC |
∴
| AC |
| BC |
| MD |
| DC |
∴MD•BC=AC•DC．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；牢固掌握定理是基础，灵活运用定理是关键；对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
如图所示，图中有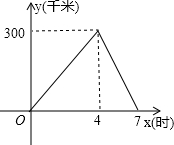
小李从甲地前往乙地，到达乙地后立刻返回，他与甲地的距离y（千米）与所用时间x（时）的函数关系如图所示．
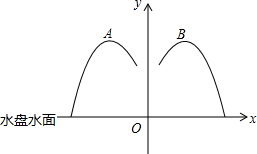一个台型喷泉，若沿着中轴线截面，得到如图所示的抛物线，一个单位长度是1米，已知这两段抛物线关于y轴对称，其右侧的抛物线为：