题目内容
在1个不透明的口袋里,装有红、白、蓝三种颜色的乒乓球(处颜色外其余都相同),其中白球有2个,黄球1个,若从中任意摸出一个球,这个球是白球的概率为
,求口袋中红球的个数?
| 1 |
| 2 |
考点:概率公式
专题:
分析:设口袋中红球的个数是m个,根据白球的概率公式列出方程求解即可.
解答:解:设口袋中红球的个数是m个,则口袋里共有2+1+m个小球,
由题意得:
=
,
解得:m=2.
答:口袋中红球的个数是5个.
由题意得:
| 2 |
| 2+1+m |
| 1 |
| 2 |
解得:m=2.
答:口袋中红球的个数是5个.
点评:本题主要考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
,难度适中.
| m |
| n |

练习册系列答案
相关题目
如果a<b,那么下列各式中正确的是( )
| A、a-2>b-2 |
| B、a-b<0 |
| C、-2a<-2b |
| D、2a>2b |
将甲班人数的
调入乙班后,甲班人数是乙班的
,那么甲班原有人数与乙班原有人数的比是( )
| 1 |
| 3 |
| 4 |
| 5 |
| A、3:2 | B、2:3 |
| C、2:1 | D、1:2 |
 用直尺和圆规作一个角的平分线(如图),则能说明∠AOC=∠BOC的依据是( )
用直尺和圆规作一个角的平分线(如图),则能说明∠AOC=∠BOC的依据是( )| A、ASA | B、AAS |
| C、HL | D、SSS |
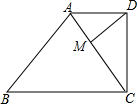 如图,已知梯形ABCD中,AD∥BC,∠ACD=∠B,过点D作DM∥AB交AC于点M.
如图,已知梯形ABCD中,AD∥BC,∠ACD=∠B,过点D作DM∥AB交AC于点M.