题目内容
15. 如图,在等腰Rt△ABC中,∠BAC=90°.将直角边足够长的Rt△EPF的直角顶点P放在线段BC的中点上,以点P为旋转中心,转动Rt△EPF并使它的两直角边PE,PF分别与AC,AB相交于点N,M,连MN,AP,交于D点,则下列几组量:
如图,在等腰Rt△ABC中,∠BAC=90°.将直角边足够长的Rt△EPF的直角顶点P放在线段BC的中点上,以点P为旋转中心,转动Rt△EPF并使它的两直角边PE,PF分别与AC,AB相交于点N,M,连MN,AP,交于D点,则下列几组量:①PM,PN;
②AM,CN;③∠NMA,∠BPM;
④∠B,∠F,
相等的有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 由条件可证明△APN≌△BPM,可判断①②;利用等腰三角直角三角形的性质结合外角的性质可判断③;利用等腰直角三角形的性质可判断④,可求得答案.
解答 解:
∵△ABC为等腰直角三角形,P这斜边BC的中点,
∴AP⊥BC,
∴∠CAP=∠B=45°,PA=PB,
∵∠APE与∠BPE均为旋转角,
∴∠APE=∠BPF=α,
在△APN和△BPM中
$\left\{\begin{array}{l}{∠NAP=∠B}\\{AP=BP}\\{∠APN=∠BPM}\end{array}\right.$
∴△APN≌△BPM(ASA),
∴PM=PN,即①相等,BM=AN,
∵AB=AC,
∴AM=CN,即②相等,
∵PM=PN,∠EPF=45°,
∴△PMN为等腰直角三角形,
∴∠NMP=∠PNM=45°,
∵∠AMP=∠MPB+∠B,∠NMP=∠B=45°,
∴∠NMP=∠BPM,即③相等,
∵△PEF不一定是等腰直角三角形,
∴∠F是否为45°不确定,
∵∠B=45°,
∴④不一定相等,
∴相等的有3组,
故选C.
点评 本题主要考查全等三角形的判定和性质及等腰直角三角形的性质,解题的关键在于找到全等三角形,得到对应的边角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.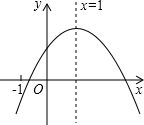 已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=1,有下列结论:①abc>0;②b2<4ac;③(a+c)2>b2 ④a<$\frac{c-b}{2}$,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=1,有下列结论:①abc>0;②b2<4ac;③(a+c)2>b2 ④a<$\frac{c-b}{2}$,其中正确结论的个数是( )
 已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=1,有下列结论:①abc>0;②b2<4ac;③(a+c)2>b2 ④a<$\frac{c-b}{2}$,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=1,有下列结论:①abc>0;②b2<4ac;③(a+c)2>b2 ④a<$\frac{c-b}{2}$,其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.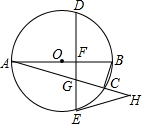 如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G,EH为⊙O的切线,交AC的延长线于H,AF=3,FB=$\frac{4}{3}$,则tan∠DEH=( )
如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G,EH为⊙O的切线,交AC的延长线于H,AF=3,FB=$\frac{4}{3}$,则tan∠DEH=( )
 如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G,EH为⊙O的切线,交AC的延长线于H,AF=3,FB=$\frac{4}{3}$,则tan∠DEH=( )
如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G,EH为⊙O的切线,交AC的延长线于H,AF=3,FB=$\frac{4}{3}$,则tan∠DEH=( )| A. | $\frac{12}{5}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
 如图,直线a∥b,△DCB中,AB与DC垂直,点A在线段BC上,直线b经过点C.若∠1=73°-∠B,求∠2的度数.
如图,直线a∥b,△DCB中,AB与DC垂直,点A在线段BC上,直线b经过点C.若∠1=73°-∠B,求∠2的度数.