题目内容
12.Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边用a、b、c表示,a=5,b=12.解这个直角三角形.(角精确到1°)分析 本题需先求出斜边的长,然后根据ab的长求出∠A的度数,从而求出∠B的度数.
解答 解:在Rt△ABC中,
∵a2+b2=c2,a=5,b=12,
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=13,
∵tanA=$\frac{a}{b}$=$\frac{5}{12}$≈0.41666,
∴∠A≈24°,
∴∠B=90°-∠A
=90°-24°
=66°.
点评 本题主要考查了解直角三角形的有关知识,在解题时要根据解直角三角形列出式子求出结果是本题的关键.

练习册系列答案
相关题目
17.若分式$\frac{|x|-3}{{x}^{2}-6x+9}$的值为0,则x的值为( )
| A. | 3 | B. | -3 | C. | 3或-3 | D. | 2或3 |
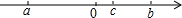 a,b,c在数轴上的位置如图所示,求|c-b|-$\sqrt{(a+b)^{2}}$-$\root{3}{(a+c)^{3}}$的值.
a,b,c在数轴上的位置如图所示,求|c-b|-$\sqrt{(a+b)^{2}}$-$\root{3}{(a+c)^{3}}$的值.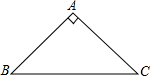 如图,在△ABC中,AB=AC,∠BAC=90°,点D为射线CB上一点,连接AD,以AD为一边在AD右侧作正方形ADEF,直线EF与直线BC交于点M,若AB=2$\sqrt{2}$,BD=1,则CM的长为$\frac{1}{2}$或$\frac{3}{2}$.
如图,在△ABC中,AB=AC,∠BAC=90°,点D为射线CB上一点,连接AD,以AD为一边在AD右侧作正方形ADEF,直线EF与直线BC交于点M,若AB=2$\sqrt{2}$,BD=1,则CM的长为$\frac{1}{2}$或$\frac{3}{2}$.