题目内容
14．当x=$\frac{3}{2}$时，代数式-2x2+6x+4有最大值，最大值=$\frac{17}{2}$．分析 把代数式-2x2+6x+4配方成a（x+b）2+c的形式，根据任何数的平方是非负数即可求解．
解答 解：-2x2+6x+4=-2（x-$\frac{3}{2}$）2+$\frac{17}{2}$，
∵-2（x-1）2≤0，
∴当x=$\frac{3}{2}$时，y最大，最大值为$\frac{17}{2}$．
故答案为：$\frac{3}{2}$，$\frac{17}{2}$．
点评 本题考查的是配方法的应用，掌握完全平方公式和非负数的性质是解题的关键，注意a2≥0．
练习册系列答案
相关题目
4．
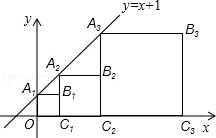正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=x+1和x轴上，则点B6的坐标是（ ）
正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=x+1和x轴上，则点B6的坐标是（ ）| A． | （63，32） | B． | （64，32） | C． | （63，31） | D． | （64，31） |
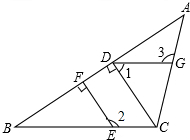如图，在△ABC中，点E、G分别在BC、AC上，CD⊥AB，EF⊥AB，垂足分别为D、F．已知∠1+∠2=180°，∠3=105°，求∠ACB的度数．
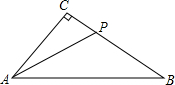已知：如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点P在BC上运动，点P不与点B，C重合，设PC=x，若用y表示△APB的面积，求y与x的函数关系式，并求自变量x的取值范围．