题目内容
20.在一个不透明的口袋中装有除颜色外其它都相同的5个红球和3个自球,任意从口袋中摸出一个球来,摸到白球的概率为$\frac{3}{8}$.分析 用白球的个数除以球的总个数即可求得摸到白球的概率.
解答 解:∵在一个不透明的口袋中装有除颜色外其它都相同的5个红球和3个白球,
∴任意从口袋中摸出一个球来,摸到白球的概率为$\frac{3}{5+3}$=$\frac{3}{8}$,
故答案为$\frac{3}{8}$.
点评 本题考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.方程2x2-2x-1=0的根的情况为( )
| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个正实数根 | D. | 有一个正实数根和一个负实数根 |
11.如果y=(m-2)${x}^{{m}^{2}-3}$+2是一次函数,那么m的值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | $±\sqrt{2}$ |
12.一项工程由甲工程队单独完成需要12天,由乙工程队单独完成需要16天,甲工程队单独施工5天后,为加快工程进度,又抽调乙工程队加入该工程施工,问还需多少天可以完成该工程?如果设还需要x天可以完成该工程,则下列方程正确的为( )
| A. | $\frac{x}{12}+\frac{x}{16}=1$ | B. | $\frac{x}{16}+\frac{5+x}{12}=1$ | C. | 12(5+x)+16x=1 | D. | 12(5+x)=16x |
9.某码头上有20名工人装载一批货物,已知每人往一艘轮船上装载2吨货物,装载完毕恰好用了6天,轮船到达目的地后,另一批工人开始卸货,计划平均每天卸货v吨,刚要卸货时遇到紧急情况,要求船上的货物卸载完毕不超过4天,则这批工人实际每天至少应卸货( )
| A. | 30吨 | B. | 40吨 | C. | 50吨 | D. | 60吨 |
10.下列各式计算正确的是( )
| A. | 2+b=2b | B. | $\sqrt{5}-\sqrt{2}=\sqrt{3}$ | C. | (2a2)3=8a5 | D. | a6÷a4=a2 |
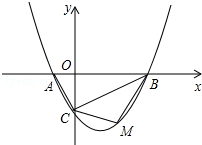 如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).