题目内容
15. 如图,四边形BFCE是平行四边形,点A、B、C、D在同一条直线上,且AB=CD,连接AE、DF.求证:AE=DF.
如图,四边形BFCE是平行四边形,点A、B、C、D在同一条直线上,且AB=CD,连接AE、DF.求证:AE=DF.
分析 根据四边形BFCE是平行四边形,得到BE=CF,BE∥CF,根据平行线的性质得到∠EBC=∠FCB,根据邻补角的定义得到∠ABE=∠DCF,根据全等三角形的性质即可得到结论.
解答 解:∵四边形BFCE是平行四边形,
∴BE=CF,BE∥CF,
∴∠EBC=∠FCB,
∵点A、B、C、D在同一条直线上,
∴∠ABE=∠DCF,
在△ABE与△DCF中,$\left\{\begin{array}{l}{AB=DC}\\{∠ABE=∠DCF}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△DCF,
∴AE=DF.
点评 此题主要考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
6.某次知识竞赛,共有20道题,每小题答对得10分,答错或不答都扣5分,小明得分要超过85分,他至少要答对( )道题.
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
3.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
| A. | 4cm | B. | 5cm | C. | 小于2cm | D. | 不大于2cm |
7.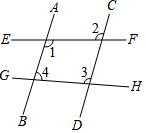 如图,下列判断中正确的是( )
如图,下列判断中正确的是( )
 如图,下列判断中正确的是( )
如图,下列判断中正确的是( )| A. | 如果EF∥GH,那么∠4+∠3=180° | B. | 如果AB∥CD,那么∠1+∠4=180° | ||
| C. | 如果AB∥CD,那么∠1=∠2 | D. | 如果AB∥CD,那么∠2=∠3 |
 解不等式7+x≥2(2x-1),并把解集在如图的数轴上表示出来.
解不等式7+x≥2(2x-1),并把解集在如图的数轴上表示出来. 如图,三条直线a,b,c两两相交,则到三条直线距离相等的点有4个.
如图,三条直线a,b,c两两相交,则到三条直线距离相等的点有4个.