题目内容
13.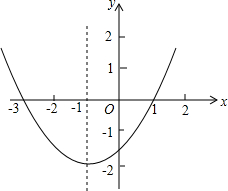 抛物线y=$\frac{1}{2}$(x+1)2-2.
抛物线y=$\frac{1}{2}$(x+1)2-2.(1)设此抛物线与x轴交点为A,B(A在B的左边),求出A、B两点的坐标;
(2)P是抛物线上的一个动点,问是否存在一点P,使S△ABP=2?若存在,则有几个这样的点P?并写出它们的坐标.
分析 (1)在抛物线的解析式中令y=0,即可求得抛物线与x轴的交点的横坐标;
(2)首先根据(1)求得AB的长,然后根据S△ABP=2,求得P的纵坐标,代入函数解析式即可求得P的坐标.
解答 解:(1)令y=0,则$\frac{1}{2}$(x+1)2-2=0,解得:x1=1,x2=-3,
则A的坐标是(-3,0),B的坐标是(1,0);
(2)AB=1-(-3)=4,
设P的纵坐标是m,则$\frac{1}{2}$×4|m|=2,
解得:|m|=1,
则m=1或-1.
当m=1时,$\frac{1}{2}$(x+1)2-2=1,解得:x=-1±$\sqrt{6}$,即P的坐标是(-1+$\sqrt{6}$,1)或(-1-$\sqrt{6}$,1);
当m=-1时,$\frac{1}{2}$(x+1)2-2=-1,解得:m=-1±$\sqrt{2}$,则P的坐标是(-1+$\sqrt{2}$,-1)或(-1-$\sqrt{2}$,-1).
总之,满足条件的P有4个,分别是:(-1+$\sqrt{6}$,1)和(-1-$\sqrt{6}$,1)和(-1+$\sqrt{2}$,-1)和(-1-$\sqrt{2}$,-1).
点评 本题考查了二次函数与x轴的交点坐标以及三角形的面积,注意到P的纵坐标有两种情况是关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
8. 综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
 综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )| A. | 12件 | B. | 8.625件 | C. | 8.5件 | D. | 9件 |
5.下列函数中,y是x的反比例函数的是( )
| A. | y=x-1 | B. | y=$\frac{8}{{x}^{2}}$ | C. | $\frac{y}{x}$=2 | D. | y=$\frac{1}{2x}$ |
2.下列运算正确的是( )
| A. | $\sqrt{9}$=-3 | B. | |-3|=-3 | C. | -$\sqrt{-9}$=-3 | D. | -32=-9 |
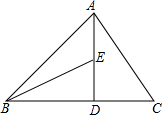 如图,在△ABC中,AD⊥BC于点D,AD=BD,DC=DE,∠C=60°,∠ABD=45°,求∠ABE的度数.
如图,在△ABC中,AD⊥BC于点D,AD=BD,DC=DE,∠C=60°,∠ABD=45°,求∠ABE的度数.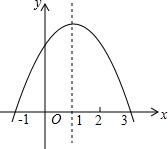 已知二次函数y=ax2+bx+c(a、b、c是常数),图象如图所示,则当x满足的条件是-1<x<3时,y>0.
已知二次函数y=ax2+bx+c(a、b、c是常数),图象如图所示,则当x满足的条件是-1<x<3时,y>0. 如图,直线l过正方形ABCD的顶点A和BC边的中点E,点B到直线l的距离1,则D到l的距离是2.
如图,直线l过正方形ABCD的顶点A和BC边的中点E,点B到直线l的距离1,则D到l的距离是2.