题目内容
 如图,在⊙O中,AB、CD是直径,CE∥AB且交圆于E,求证:
如图,在⊙O中,AB、CD是直径,CE∥AB且交圆于E,求证: |
| BD |
 |
| BE |
考点:圆心角、弧、弦的关系
专题:证明题
分析:首先连接OE,由CE∥AB,可证得∠DOB=∠C,∠BOE=∠E,然后由OC=OE,可得∠C=∠E,继而证得∠DOB=∠BOE,则可证得:
=
.
 |
| BD |
 |
| BE |
解答: 证明:连接OE,
证明:连接OE,
∵CE∥AB,
∴∠DOB=∠C,∠BOE=∠E,
∵OC=OE,
∴∠C=∠E,
∴∠DOB=∠BOE,
∴
=
.
 证明:连接OE,
证明:连接OE,∵CE∥AB,
∴∠DOB=∠C,∠BOE=∠E,
∵OC=OE,
∴∠C=∠E,
∴∠DOB=∠BOE,
∴
 |
| BD |
 |
| BE |
点评:此题考查了圆心角与弧的关系以及平行线的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
小刚做了一道数学题:“已知两个多项式为A,B,求A+B的值,”他误将“A+B”看成了“A-B”,结果求出的答案是x-y,若已知B=3x-2y,那么原来A+B的值应该是( )
| A、4x+3y | B、2x-y |
| C、-2x+y | D、7x-5y |
 如图,从正面看由相同的小正方体搭成的几何体,所得到的平面图形是( )
如图,从正面看由相同的小正方体搭成的几何体,所得到的平面图形是( )A、 |
B、 |
C、 |
D、 |
 如图,A,B,C是⊙O上的三个点,若∠C=35°,则∠AOB的度数为( )
如图,A,B,C是⊙O上的三个点,若∠C=35°,则∠AOB的度数为( )| A、35° | B、55° |
| C、65° | D、70° |
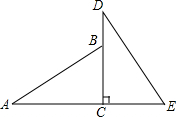 如图,A、C、E在一条直线上,DC⊥AE,垂足为C.已知AB=DE,若根据“HL”,△ABC≌△DEC,则可添加条件为
如图,A、C、E在一条直线上,DC⊥AE,垂足为C.已知AB=DE,若根据“HL”,△ABC≌△DEC,则可添加条件为