题目内容
如图,半圆O的直径AB长度为6,半径OC⊥AB,沿OC将半圆剪开得到两个圆心角为90°的扇形.将右侧扇形向左平移,使得点A与点O′,点O与点B分别重合,则所得图形中重叠部分的面积为 .


考点:扇形面积的计算
专题:
分析:连接AE,作ED⊥AB于点D,S扇形-S△ADE,即可求得弧BE和BD以及DE围成的阴影部分的面积,则阴影部分的面积即可求得.
解答: 解:连接AE,作ED⊥AB于点D.
解:连接AE,作ED⊥AB于点D.
∵AE=AB=2AD,
∴∠AED=30°,
∴∠EAB=60°,
∴S扇形=
=
π,
在直角△ADE中,DE=
=
=
,则S△ADE=
×
×
=
,
则弧BE和BD以及DE围成的阴影部分的面积是:
π-
,
则S阴影=2(
π-
)=3π-
.
故答案是:3π-
.
 解:连接AE,作ED⊥AB于点D.
解:连接AE,作ED⊥AB于点D.∵AE=AB=2AD,
∴∠AED=30°,
∴∠EAB=60°,
∴S扇形=
| 60π×32 |
| 360 |
| 3 |
| 2 |
在直角△ADE中,DE=
| AE2-AD2 |
32-(
|
3
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
9
| ||
| 8 |
则弧BE和BD以及DE围成的阴影部分的面积是:
| 3 |
| 2 |
9
| ||
| 8 |
则S阴影=2(
| 3 |
| 2 |
9
| ||
| 8 |
9
| ||
| 4 |
故答案是:3π-
9
| ||
| 4 |
点评:本题考查了扇形的面积的计算,正确理解不规则的图形的面积转化为规则图形的面积的和、差计算,是关键.

练习册系列答案
相关题目
下列变形中,正确的是( )
| A、若5x-6=7,则5x-7=-6 | ||
B、若-
| ||
C、若
| ||
D、若-3x=5,则x=-
|
抛物线y=(x-1)2+2的顶点坐标是( )
| A、(1,2) |
| B、(1,-2) |
| C、(-1,2) |
| D、(-1,-2) |
若方程2x3-5m+5(m-1)=0是关于x的一元一次方程,则这个方程的解是( )
A、
| ||
B、-
| ||
C、
| ||
| D、3 |
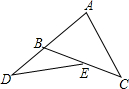 如图,∠A,∠DBC,∠DEC的大小关系是( )
如图,∠A,∠DBC,∠DEC的大小关系是( )| A、∠A>∠DBC>∠DEC |
| B、∠DEC>∠A>∠DBC |
| C、∠DEC>∠DBC>∠A |
| D、∠DBC>∠A>∠DEC |
一个矩形的长比宽相多3cm,面积是25cm2,求这个矩形的长和宽.设矩形的宽为xcm,则所列方程正确的是( )
| A、x2-3x+25=0 |
| B、x2-3x-25=0 |
| C、x2+3x-25=0 |
| D、x2+3x-50=0 |
 如图,在⊙O中,AB、CD是直径,CE∥AB且交圆于E,求证:
如图,在⊙O中,AB、CD是直径,CE∥AB且交圆于E,求证: