题目内容
17. 如图所示,CD为⊙O的弦,在CD上取CE=DF,连结OE、OF,并延长交⊙O于点A、B.
如图所示,CD为⊙O的弦,在CD上取CE=DF,连结OE、OF,并延长交⊙O于点A、B.(1)试判断△OEF的形状,并说明理由;
(2)求证:$\widehat{AC}$=$\widehat{BD}$.
分析 (1)首先连接OC,OD,由CE=DF,利用SAS,即可证得△OCE≌△ODF,继而判定△OEF是等腰三角形;
(2)由△OCE≌△ODF,可证得∠COE=∠DOF,然后由圆心角与弧的关系,证得结论.
解答 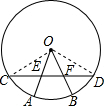 (1)解:△OEF是等腰三角形,
(1)解:△OEF是等腰三角形,
理由:连接OC,OD,
∵OC=OD,
∴∠C=∠D,
在△OCE和△ODF中,
$\left\{\begin{array}{l}{OC=OD}\\{∠C=∠D}\\{CE=DF}\end{array}\right.$,
∴△OCE≌△ODF(SAS),
∴OE=OF,
即△OEF是等腰三角形;
(2)证明:∵△OCE≌△ODF,
∴∠COE=∠DOF,
∴$\widehat{AC}$=$\widehat{BD}$.
点评 此题考查了弧与圆心角的关系以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
9.在现实生活中,用地砖铺地,用瓷砖贴膜,都要求砖于砖之间严丝合缝、不留空隙、不能重叠,这些工作从数学的角度解释,就叫用多边形覆盖平面(或平面镶嵌),下面不能用于平面镶嵌的图形是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
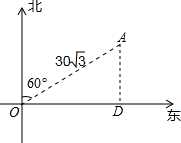 如图,在A岛周围20海里水域内有暗礁,一轮船由西向东航行到O处时,测得A岛在北偏东60°的方向,且与轮船相距30$\sqrt{3}$海里.若该船继续保持由西向东的航向,那么有触礁的危险吗?
如图,在A岛周围20海里水域内有暗礁,一轮船由西向东航行到O处时,测得A岛在北偏东60°的方向,且与轮船相距30$\sqrt{3}$海里.若该船继续保持由西向东的航向,那么有触礁的危险吗?