题目内容
如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD= 米(结果可保留根号)

21+7
考点: 解直角三角形的应用-仰角俯角问题.
分析: 作AE⊥CD于点E,则△AED和△ABD都是等腰直角三角形,即可求得DE的长,然后在直角三角形中利用三角函数求得CE的长,进而求得CD的长.
解答: 解:作AE⊥CD于点E.
在直角△ABD中,∠ADB=45°,
∴DE=AE=BD=AB=21(米),
在直角△AEC中,CE=AE•tan∠CAE=21× =7
=7 (米).
(米).
则CD=(21+7 )米.
)米.
故答案是:21+7 .
.

点评: 本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出 部分频数分布表和部分频数分布直方图如图表:
部分频数分布表和部分频数分布直方图如图表:
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 6 |
| 第2组 | 30≤x<35 | 8 |
| 第3组 | 35≤x<40 | 16 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 8 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则
本次测试的优秀率是多少?
(4)第5组8名同学中,有4名男同学,
现将这8名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小亮与小华两名男同学分在同一组的概率.

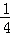 B.
B. 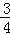 C.
C.  D. 1
D. 1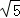 ,则tan∠CAD的值是( )
,则tan∠CAD的值是( )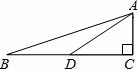
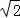 C.
C.  D.
D. 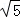
 的图象大致如图.若y1<y2,则自变量x的取值范围是( )
的图象大致如图.若y1<y2,则自变量x的取值范围是( )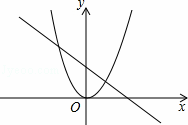
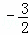 <x<2 B. x>2或x<
<x<2 B. x>2或x<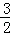 D. x<﹣2或x>
D. x<﹣2或x>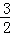

 ,1中,最小的实数是( )
,1中,最小的实数是( )