题目内容
如图1,已知△ABC是等腰直角三角形,∠BAC=90°,AD是BC边上的高,延长BC至点E,以D为圆心,DE为半径作圆弧EF,使点A在DF上,连接AE、BF.
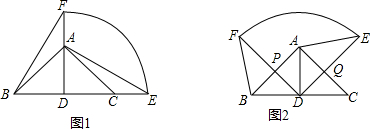
(1)试猜想线段AE和BF的数量关系,并写出你的结论;
(2)将扇形DEF绕点D按逆时针方向旋转一定角度后(旋转角大于0°且小于180°),DF、DE分别交AB、AC于点P、Q.如图2,则(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
(3)在(2)的条件下,请连接EF、PQ,求证:EF∥PQ且AE⊥BF.
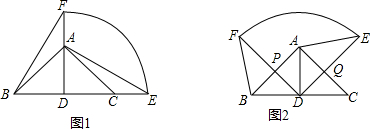
(1)试猜想线段AE和BF的数量关系,并写出你的结论;
(2)将扇形DEF绕点D按逆时针方向旋转一定角度后(旋转角大于0°且小于180°),DF、DE分别交AB、AC于点P、Q.如图2,则(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
(3)在(2)的条件下,请连接EF、PQ,求证:EF∥PQ且AE⊥BF.
考点:几何变换综合题
专题:
分析:(1)根据等腰直角三角形斜边上的高就是中线,得出AD=BD=DC,因为DF和DE是圆的半径所以相等,根据SAS即可求得;
(2)根据旋转的性质得出∠BDF=∠ADE,然后根据SAS即可求得;
(3)根据三角形求得得出∠BFD=∠AED,根据对顶角相等得出∠FHG=∠EHD,根据等量加等量还是等量得出∠FGE=90°,再求出A、P、D、Q四点共圆,然后根据圆周角的性质得出∠DPQ=∠DAQ=45°,因为∠EFD=45°,根据同位角相等两直线平行即可证得;
(2)根据旋转的性质得出∠BDF=∠ADE,然后根据SAS即可求得;
(3)根据三角形求得得出∠BFD=∠AED,根据对顶角相等得出∠FHG=∠EHD,根据等量加等量还是等量得出∠FGE=90°,再求出A、P、D、Q四点共圆,然后根据圆周角的性质得出∠DPQ=∠DAQ=45°,因为∠EFD=45°,根据同位角相等两直线平行即可证得;
解答:
(1)AE=BF,
证明:如图1,∵△ABC是等腰直角三角形,∠BAC=90°,AD是BC边上的高,
∴AD=BD=DC,
在△BDF与△ADE中
∴△BDF≌△ADE(SAS),
∴AE=BF;

(2)成立;
证明:如图2,∵∠ADF=∠CDE,AD⊥BC,
∠BDF=∠ADE,
由(1)可知AD=BD,
在△BDF与△ADE中
∴△BDF≌△ADE(SAS),
∴AE=BF;
(3)如图2,连接PQ,、EF,延长EA交BF于G,交DF于H,由(2)可知△BDF≌△ADE,
∴∠BFD=∠AED,
∵∠FHG=∠EHD,
∴∠BFD+∠FHG=∠AED+∠EHD,
∵∠AED+∠EHD=90°,
∴∠BFD+∠FHG=90°,
∴∠FGE=90°,
即AE⊥BF.
∵∠BAC=∠EDF=90°,
∴A、P、D、Q四点共圆,
∴∠DPQ=∠DAQ=45°,
∵DF=DE,∠EDF=90°,
∴∠EFD=45°,
∴∠EFD=∠QPD=45°,
∴EF∥PQ.

(1)AE=BF,
证明:如图1,∵△ABC是等腰直角三角形,∠BAC=90°,AD是BC边上的高,
∴AD=BD=DC,
在△BDF与△ADE中
|
∴△BDF≌△ADE(SAS),
∴AE=BF;

(2)成立;
证明:如图2,∵∠ADF=∠CDE,AD⊥BC,
∠BDF=∠ADE,
由(1)可知AD=BD,
在△BDF与△ADE中
|
∴△BDF≌△ADE(SAS),
∴AE=BF;
(3)如图2,连接PQ,、EF,延长EA交BF于G,交DF于H,由(2)可知△BDF≌△ADE,
∴∠BFD=∠AED,
∵∠FHG=∠EHD,
∴∠BFD+∠FHG=∠AED+∠EHD,
∵∠AED+∠EHD=90°,
∴∠BFD+∠FHG=90°,
∴∠FGE=90°,
即AE⊥BF.
∵∠BAC=∠EDF=90°,
∴A、P、D、Q四点共圆,
∴∠DPQ=∠DAQ=45°,
∵DF=DE,∠EDF=90°,
∴∠EFD=45°,
∴∠EFD=∠QPD=45°,
∴EF∥PQ.
点评:本题考查了等腰直角三角形的性质,圆的性质,旋转的性质以及三角形求得的判定和性质;四点共圆是本题的难点.

练习册系列答案
相关题目
 如图,在4×4正方形网格中,每个小正方形的边长都为1.
如图,在4×4正方形网格中,每个小正方形的边长都为1. 已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE.
已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2,求证:∠B=∠ADE.  如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,
如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度, 如图,△ABC中,点D在BC的延长线上,若∠ACD=100°,∠A=40°,则∠B的度数是
如图,△ABC中,点D在BC的延长线上,若∠ACD=100°,∠A=40°,则∠B的度数是