题目内容
在△ABC内侧作射线 ,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.
,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.
(1)依题意补全图1;
(2)求证:MD=ME;
(3)如图2,若射线AP平分∠BAC,且AC>AB,求证:MD=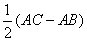 .
.
 | |||
 | |||
解:(1)补全图形,如图1所示. ……… 1分
(2)延长DM交CE于点F.
∵BD、CE分别垂直AP于点D、E.
∴BD∥CE.,∴∠1= ∠2.
∵M为BC边中点,
∴BM=CM, 又∵∠DMB= ∠FMC,
∴△DMB≌△FMC (ASA),
∴DM=FM.
∵∠DEF=90°.
∴EM=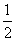 DF,
DF,
∴MD=ME.
 | |||
 | |||
(3)延长BD交AC于点G.
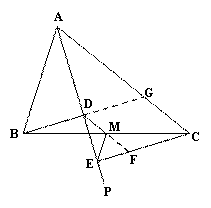 ∵BD⊥AP于点D,射线AP平分∠BAC,
∵BD⊥AP于点D,射线AP平分∠BAC,
∴△ADB≌△ADG (ASA),
∴BD=DG,AB=AG.
又∵△DMB≌△FMC,
∴BD=CF,DM=MF,
∴CF=DG,
又∵BG∥CF,
∴四边形DFCG为平行四边形.
∴DF=CG,
∴2MD=CG,
∴2MD=AC-AB,
∴MD=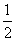 (AC-AB).
(AC-AB).

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,那么分式
,那么分式 的值等于
的值等于  度.
度. ∠ABC=90°,AB=5,AD=4.求对角线AC的长.
∠ABC=90°,AB=5,AD=4.求对角线AC的长.

 BC,则△ABC底角的度数为__________.
BC,则△ABC底角的度数为__________. ,∠ACP=45°时,求AB的长.
,∠ACP=45°时,求AB的长. 
 的值是( )
的值是( )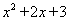 的值,我们必须知道
的值,我们必须知道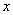 的值.若
的值.若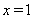 ,则这个代数式的值为_______;若
,则这个代数式的值为_______;若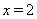 ,则这个代数式的值为__
,则这个代数式的值为__ _____,……,可见,这个代数式的值因
_____,……,可见,这个代数式的值因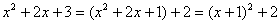 ,因为
,因为 是非负数,所以,这个代数式
是非负数,所以,这个代数式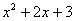 的最小值是_______,这时
的最小值是_______,这时 相应的
相应的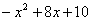 的最大(或最小)值,并写出相应的
的最大(或最小)值,并写出相应的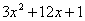 的最大(或最小)值,并写出相应的
的最大(或最小)值,并写出相应的 ,且
,且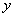 的变化范围.
的变化范围. ,则由题意可列方程为( )
,则由题意可列方程为( ) B.
B. 
 D.
D. 
