题目内容
如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.
(1)求证:PB+PC>2AB.
(2)当PC=2,PB= ,∠ACP=45°时,求AB的长.
,∠ACP=45°时,求AB的长.

解:(1)如图,在射线BA上取点B'使AB’=AB,连接PB’,
∵P为等腰△ABC的外角平分线上任一点,∴∠B’AP=∠CAP,AB=AC,AB’=AC,
 ∵PA=PA,∴△B’AP≌△CAP,∴PB’=PC.
∵PA=PA,∴△B’AP≌△CAP,∴PB’=PC.
在△B’BP中,∵PB+PB’>BB’
∴PB+PC>2AB. ………………………………3分
(2)在△B’BP中,作PH⊥BB’于点H,
∵△B’AP≌△CAP,∴∠PB’A=∠PCA=45°,
∵PC=2,∴PB’=2.∴B’H=PH= .
.
在Rt△PHB中,∵PB= ,
,
利用勾股定理解得BH= ,
,
∴BB’= ,
,
∴AB的长为 ………………………………5分
………………………………5分

练习册系列答案
相关题目
 ②
② ③
③ ④
④ 
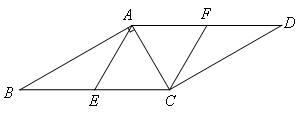


 ,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.
,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.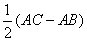 .
.


