题目内容
1.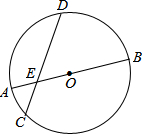 如图所示,⊙O的直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=60°,求弦CD的长.
如图所示,⊙O的直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=60°,求弦CD的长.
分析 作OF⊥CD于点F,连接OD,直角△OEF中利用三角函数即可求得OF的长,然后在直角△ODF中利用勾股定理即可求得DF的长,然后根据垂径定理可以得到CD=2DF,从而求解.
解答 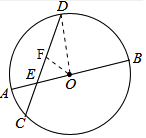 解:作OF⊥CD于点F,连接OD.
解:作OF⊥CD于点F,连接OD.
∵AE=2,EB=6,
∴AB=AE+BE=8,半径长是4.
∵在直角△OEF中,OE=OA-AE=4-2=2,
sin∠DEB=$\frac{OF}{OE}$,
∴OF=OE•sin∠DEB=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
在直角△ODF中,
∵DF=$\sqrt{O{D}^{2}-O{F}^{2}}$=$\sqrt{13}$,
∴CD=2DF=2$\sqrt{13}$.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
16.下列计算正确的是( )
| A. | 4x2-2x2=2 | B. | x+x=x2 | C. | 4x6÷2x2=2x3 | D. | x•x2=x3 |
12.已知,k=$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{b+c-a}{a}$,则k的值为( )
| A. | $\frac{2}{3}$ | B. | 3 | C. | 1或-2 | D. | $\frac{3}{2}$ |
13.下列叙述正确的是( )
| A. | 平分弦的直径垂直于弦 | B. | 三角形的外心到三边的距离相等 | ||
| C. | 三角形的内心到三边的距离相等 | D. | 相等的圆周角所对的弧相等 |
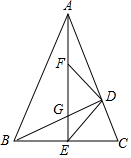 已知:如图,在△ABC中,∠BAC=45°,BD、AE分别是边AC、BC边上的高,AE和BD交于点G,点E、点F分别是BC、AG的中点.判断△DEF的形状,并说明理由.
已知:如图,在△ABC中,∠BAC=45°,BD、AE分别是边AC、BC边上的高,AE和BD交于点G,点E、点F分别是BC、AG的中点.判断△DEF的形状,并说明理由.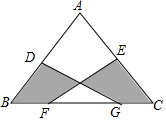 如图,在△ABC中,AB=AC=10,BC=12,D、E分别为AB,AC中点,F、G为线段BC上两点,且FG=6,则阴影部分面积为24.
如图,在△ABC中,AB=AC=10,BC=12,D、E分别为AB,AC中点,F、G为线段BC上两点,且FG=6,则阴影部分面积为24.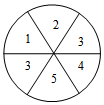 “六•一”儿童节,学校举办文艺汇演活动,小丽和小芳都相当节目主持人,但现在只有一个名额.小丽想出了一个办法,她将一个转盘(均质的)均分成6份,若图所示,游戏规定:随意转动转盘,若指针指到3,则小丽去;若指针指到2,则小芳去,这个游戏公平吗?为什么?
“六•一”儿童节,学校举办文艺汇演活动,小丽和小芳都相当节目主持人,但现在只有一个名额.小丽想出了一个办法,她将一个转盘(均质的)均分成6份,若图所示,游戏规定:随意转动转盘,若指针指到3,则小丽去;若指针指到2,则小芳去,这个游戏公平吗?为什么?