题目内容
13.我们规定两数a、b之间的一种运算,记作[a,b]:如果ac=b,那么[a,b]=c例如[2,8]=3,对于任意自然数n,可以证明[3n,4n]=[3,4],理由如下:设[3n,4n]=x,则(3n)x=4n,∴(3x)n=4n,∴3x=4,∴[3,4]=x,∴[3n,4n]=[3,4].
(1)根据以上规定求出:[4,64]=3;[2014,1]=0;
(2)说明等式[3,3]+[3,5]=[3,15]成立的理由;并计算[5,2]+[5,7]=[5,14];
(3)猜想:[4,12]-[4,2]=[4,6],并说明理由.
分析 (1)根据题意如果ac=b,那么[a,b]=c,进而将原式变形求出答案;
(2)根据[3,3]与[3,5]的意义,得出[3,3]+[3,5],再表示出[3,15]的值进而得出答案;表示出[5,2]与[5,7]的值进而得出答案;
(3)利用同底数幂的除法运算法则将原式变形求出答案.
解答 解:(1)设[4,64]=x,则4x=64=43,
故x=3,即[4,64]=3;
设[2014,1]=x,则2014x=1=20140,
故x=0,即[2014,1]=0;
故答案为:3,0;
(2)设[3,3]=m,[3,5]=n,则3m=3,3n=5,
故3m•3n=3m+n=3×5=15,
则[3,15]=m+n,
即[3,3]+[3,5]=[3,15],
设[5,2]=m,[5,7]=n,则5m=2,5n=7,
故5m×5n=5m+n=2×7=14,
则[5,14]=m+n,
即[5,2]+[5,7]=[5,14];
故答案为:14;
(3)设[4,12]=m,[4,2]=n,则4m=12,4n=2,
故$\frac{{4}^{m}}{{4}^{n}}$=4m-n=$\frac{12}{2}$=6,
则[4,6]=m-n,
即[4,12]-[4,2]=[4,6].
故答案为:6.
点评 此题主要考查了同底数幂的乘除运算法则,正确将原式变形分析是解题关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
1. 如图,A,O,B在一条直线上,∠1=∠2,∠3=∠4,则图中互余的角共有( )
如图,A,O,B在一条直线上,∠1=∠2,∠3=∠4,则图中互余的角共有( )
 如图,A,O,B在一条直线上,∠1=∠2,∠3=∠4,则图中互余的角共有( )
如图,A,O,B在一条直线上,∠1=∠2,∠3=∠4,则图中互余的角共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
5.在-(-8),-|-7|,-|0|,(-2)2,-32这四个数中,非负数共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
2.在下列实数中,无理数是( )
| A. | 3.1415926 | B. | $\frac{22}{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{\frac{4}{9}}$ |
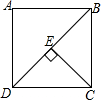 如图,设矩形ABCD的边BC=x,DC=y,连接BD且CE⊥BD,CE=2,BD=4,则(x+y)2-3xy+2的值为10.
如图,设矩形ABCD的边BC=x,DC=y,连接BD且CE⊥BD,CE=2,BD=4,则(x+y)2-3xy+2的值为10.
 已知:∠AOB,求作:∠COD,使∠COD=2∠AOB.
已知:∠AOB,求作:∠COD,使∠COD=2∠AOB.