题目内容
 如图,Rt△ABC和Rt△DCE的斜边长相等,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,连接DB,则∠EDB的度数为( )
如图,Rt△ABC和Rt△DCE的斜边长相等,其中∠ACB=∠CED=90°,∠A=45°,∠CDE=30°,∠BCE=15°,连接DB,则∠EDB的度数为( )| A、10° | B、20° |
| C、7.5° | D、15° |
考点:等腰直角三角形
专题:
分析:设AB、CD相交于点F,根据直角三角形两锐角互余求出∠BCD=45°,再根据等腰直角三角形的性质可得CF=BF=
AB,CF⊥AB,再求出DF=BF,然后根据等腰三角形两底角相等列式计算即可求出∠FDB,然后由∠EDB=∠FDB-∠CDE即可求出∠EDB的度数.
| 1 |
| 2 |
解答:解:如图,设AB、CD相交于点F,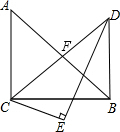
∵∠CED=90°,∠CDE=30°,∠BCE=15°,
∴∠BCD=90°-30°-15°=45°,
∵∠ACB=90°,∠A=45°,
∴△ABC是等腰直角三角形,
∴CF=BF=
AB,CF⊥AB,
∵AB=CD,
∴DF=BF=
AB,
∴∠BDF=
(180°-90°)=45°,
∴∠BDE=∠BDF-∠CDE=45°-30°=15°.
故选D.

∵∠CED=90°,∠CDE=30°,∠BCE=15°,
∴∠BCD=90°-30°-15°=45°,
∵∠ACB=90°,∠A=45°,
∴△ABC是等腰直角三角形,
∴CF=BF=
| 1 |
| 2 |
∵AB=CD,
∴DF=BF=
| 1 |
| 2 |
∴∠BDF=
| 1 |
| 2 |
∴∠BDE=∠BDF-∠CDE=45°-30°=15°.
故选D.
点评:本题考查了三角形的内角和定理,等腰直角三角形的判定与性质,解题的关键在于判断出△ABC是等腰直角三角形并求出BF=DF.

练习册系列答案
相关题目
 若有理数a,b,c在数轴上的位置如图所示,在下列结论中:①a-b>0②ab<0③a+b<0④b(a-c)>0,其中正确的个数有( )
若有理数a,b,c在数轴上的位置如图所示,在下列结论中:①a-b>0②ab<0③a+b<0④b(a-c)>0,其中正确的个数有( )| A、1个 | B、2个 | C、3个 | D、4个 |
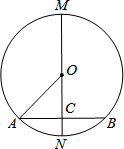 如图,⊙O的直径MN垂直弦AB于点C,若OM=5cm.下列结论中可能成立的是( )
如图,⊙O的直径MN垂直弦AB于点C,若OM=5cm.下列结论中可能成立的是( )| A、AB=12cm |
| B、OC=6cm |
| C、MN=8cm |
| D、AC=2.5cm |
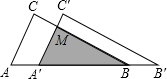 如图所示,把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半,若AB=
如图所示,把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半,若AB=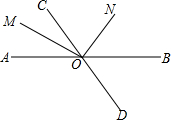 如图,OM平分∠AOC,OM⊥ON,∠BOD=70°,求∠CON.
如图,OM平分∠AOC,OM⊥ON,∠BOD=70°,求∠CON.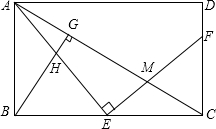 如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.