题目内容
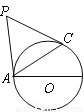
已知:如图,在 △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
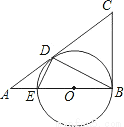
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
(1)证明见解析;(2)证明见解析. 【解析】 试题分析:从切线的性质出发,通过切线与弦所夹的角与弧弦夹角相等,即得到∠CDB=∠CBA;由切线的性质而求得. 试题解析:(1)证明:∵∠ABC=90°, ∴OB⊥BC ∵OB是⊙O的半径, ∴CB为⊙O的切线. 又∵CD切⊙O于点D, ∴BC=CD; (2)证明:∵BE是⊙O的直径, ∴∠...
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目


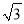 ,-9),则其解析式为_______________。
,-9),则其解析式为_______________。
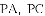
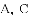
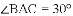
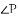
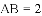
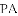
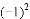 ,
,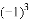 ,
,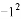 ,
,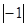 ,-(-1),
,-(-1),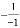 中,其中等于1的个数是( )
中,其中等于1的个数是( )