Question

如图，AB是⊙O的直径，P为AB延长线上的一个动点，过点P作⊙O的切线，切点为C，连接AC，BC，作∠APC的平分线交AC于点D．

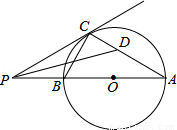
下列结论正确的是 （写出所有正确结论的序号）

①△CPD∽△DPA；

②若∠A=30°，则PC=BC；

③若∠CPA=30°，则PB=OB；

④无论点P在AB延长线上的位置如何变化，∠CDP为定值．

Answer 1

②③④

【解析】

试题分析：【解析】
①∵∠CPD=∠DPA，∠CDP=∠DAP+∠DPA≠∠DAP≠∠PDA，

∴△CPD∽△DPA错误；

②连接OC，

∵AB是直径，∠A=30°

∴∠ABC=60°，

∴OB=OC=BC，

∵PC是切线，

∴∠PCB=∠A=30°，∠OGP=90°，

∴∠APC=30°，

∴在RT△POC中，cot∠APC=cot30°=，

∴PC=BC，正确；

③∵∠ABC=∠APC+∠PCB，∠PCB=∠A，

∴∠ABC=∠APC+∠A，

∵∠ABC+∠A=90°，

∴∠APC+2∠A=90°，

∵∠APC=30°，

∴∠A=∠PCB=30°，

∴PB=BC，∠ABC=60°，

∴OB=BC=OC，

∴PB=OB；正确；

④【解析】
如图，连接OC，

∵OC=OA，PD平分∠APC，

∴∠CPD=∠DPA，∠A=∠ACO，

∵PC为⊙O的切线，

∴OC⊥PC，

∵∠CPO+∠COP=90°，

∴（∠CPD+∠DPA）+（∠A+∠ACO）=90°，

∴∠DPA+∠A=45°，

即∠CDP=45°；正确；

故答案为：②③④

考点：切线的性质；三角形的角平分线、中线和高；三角形的外角性质；相似三角形的判定与性质