题目内容
(6分)如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是。(结果保留 )
)

【解析】
连接AD,如图,

∵⊙A与BC相切于点D,
∴AD⊥BC,且AD=2,
又∵∠EAF=2∠EPF=80°,
而BC=4,
∴S阴=S△ABC﹣S扇EAF= BC×AD﹣
BC×AD﹣ =4﹣
=4﹣
【解析】
试题分析:连接AD,根据切线的性质得AD⊥BC,即AD=2为BC边上的高;再根据圆周角定理得∠EAF=2∠EPF=80°,而S阴=S△ABC﹣S扇EAF,然后利用扇形的面积公式:S= 和三角形的面积公式即可计算出图中阴影部分的面积
和三角形的面积公式即可计算出图中阴影部分的面积
考点:扇形面积的计算;切线的性质

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 的值也是负整数,写出一个符合条件的X的值 .
的值也是负整数,写出一个符合条件的X的值 . 的根,则该三角形的周长是
的根,则该三角形的周长是
 圆周的一个扇形,将留下的扇形围成一个圆锥(接线处不重叠),那么这个圆锥的高是________cm。
圆周的一个扇形,将留下的扇形围成一个圆锥(接线处不重叠),那么这个圆锥的高是________cm。
 =50 B.20(1﹣x)
=50 B.20(1﹣x) =50
=50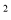 =20 D.50(1﹣x)
=20 D.50(1﹣x) =20
=20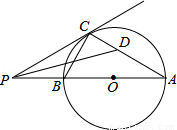
 BC;
BC;