题目内容
（本题满分7分）已知：如图，
内接于⊙
，点
在
的延长线上，
．
（1）求证：
是⊙
的切线；（2）若
，
，求
的长．
（1）证明
即可，过程略；（2）
【解析】
试题分析：（1）根据圆切线的定义，需证明
，故需先联结
，再证明
，根据同弧所对的圆心角是圆周角的两倍、
、
，可得
是等边三角形，故可证得；（2）由垂径定理知
，结合（1）中的结论和含
直角三角形的三边关系可求得
长.
试题解析：（1）联结
， 
是等边三角形 
是⊙
的切线
（2）
是等边三角形 
在
中，
，
考点：1.圆切线的判定及性质；2.垂径定理；3.含
的直角三角形的性质.
练习册系列答案
春雨教育同步作文系列答案
相关题目
中，
,
与
，
与
，若
，
，则
（ ）.
B．
C．
D．
＋2x＋6=0是一元二次方程．
、
是方程
的两个实数根，不解方程，求下列代数式的值．
； （2）
的地图上，测得
、
两地间的图上距离为
厘米，则其实际距离为
㎝．则图中阴影部分的面积是 ．
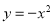向左平移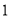
个单位，然后向上平移
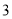个单位，则平移后抛物线的解析式为（ ）．
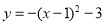B．
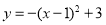D．