题目内容
阅读下列材料:
我们知道 的几何意义是在数轴上数
的几何意义是在数轴上数 对应的点与原点的距离;即
对应的点与原点的距离;即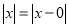 ;这个结论可以推广为
;这个结论可以推广为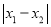 表示在数轴上数
表示在数轴上数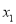 ,
, 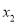 对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
例1:解方程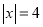 .
.
容易得出,在数轴上与原点距离为4的点对应的数为±4,即该方程的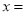 ±4;
±4;
例2:解方程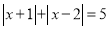 .
.
由绝对值的几何意义可知,该方程表示求在数轴上与-1和2的距离之和为5的点对应的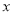 的值.在数轴上,-1和2的距离为3,满足方程的
的值.在数轴上,-1和2的距离为3,满足方程的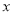 对应的点在2的右边或在-1的左边.若
对应的点在2的右边或在-1的左边.若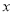 对应的
对应的
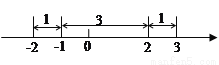
点在2的右边,如图可以看出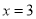 ;同理,若
;同理,若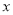 对应点在-1的左边,可得
对应点在-1的左边,可得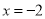 .所以原方程的解是
.所以原方程的解是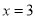 或
或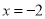 .
.
例3:解不等式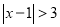 .
.
在数轴上找出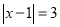 的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的
的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的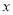 值就满足
值就满足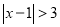 ,所以
,所以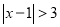 的解为
的解为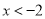 或
或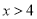 .
.
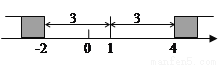
参考阅读材料,解答下列问题:
(1)方程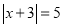 的解为 ;
的解为 ;
(2)方程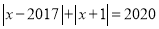 的解为 ;
的解为 ;
(3)若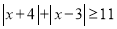 ,求
,求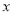 的取值范围.
的取值范围.
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目


 C. ﹣
C. ﹣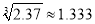 ,
, 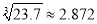 ,那么
,那么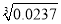 约等于( ).
约等于( ).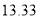 B.
B. 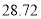 C.
C. 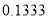 D.
D. 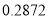
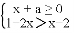 有解,则a的取值范围是( )
有解,则a的取值范围是( )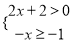 的解集在数轴上表示,正确的结果是( )
的解集在数轴上表示,正确的结果是( )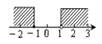 B.
B. 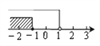 C.
C. 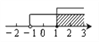 D.
D. 
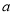 ,三角形的高为
,三角形的高为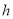 .
.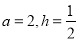 时,求阴影部分的面积.
时,求阴影部分的面积.