题目内容
3.请写出一个解为$\left\{\begin{array}{l}{x=3}\\{y=-4}\end{array}\right.$的二元一次方程组,这个方程组可以是$\left\{\begin{array}{l}{x+y=-1}\\{x-y=7}\end{array}\right.$.分析 所谓方程组的解,指的是该数值满足方程组中的每一方程.在求解时,应先围绕$\left\{\begin{array}{l}{x=3}\\{y=-4}\end{array}\right.$列一组算式,然后用x,y代换即可列不同的方程组.
解答 解:先围绕$\left\{\begin{array}{l}{x=3}\\{y=-4}\end{array}\right.$列一组算式
如3-4=-1,3+4=7.
然后用x,y代换
得$\left\{\begin{array}{l}{x+y=-1}\\{x-y=7}\end{array}\right.$等.
故答案为$\left\{\begin{array}{l}{x+y=-1}\\{x-y=7}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,是开放性试题,答案不唯一.要学生理解方程组的解的定义,围绕解列不同的算式即可列不同的方程组.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
18.已知方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx+2y=10}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,但杨岚同学在解该题时,看错了c,结果求出的解为$\left\{\begin{array}{l}{x=4}\\{y=9}\end{array}\right.$则a,b,c的值分别为( )
| A. | 5,-2,1 | B. | 5,-2,-1 | C. | -5,-2,1 | D. | -5,-2,-1 |
12.若关于x的方程$\frac{2}{x-2}$+$\frac{m}{2-x}=1$的解为正数,则m的取值范围是( )
| A. | m<4 | B. | m>4 | C. | m<4且m≠2 | D. | m>0且m≠2 |
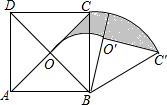 如图,正方形ABCD中,对角线AC、BD相交于点O,△OBC绕点B顺时针旋转60°得到△0′BC′,若AB=2,则图中阴影部分的面积是 $\frac{π}{3}$.
如图,正方形ABCD中,对角线AC、BD相交于点O,△OBC绕点B顺时针旋转60°得到△0′BC′,若AB=2,则图中阴影部分的面积是 $\frac{π}{3}$.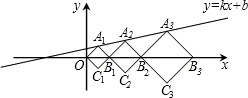 在平面直角坐标系xOy中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2按图中所示的方式放置,点A1、A2、A3…和B1、B2、B3…分别在直线y=kx+b和x轴上,如果A1(1,-1),A2($\frac{7}{2}$,$\frac{3}{2}$),则点A2016的坐标是(5×($\frac{3}{2}$)2015-4,($\frac{3}{2}$)2015).
在平面直角坐标系xOy中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2按图中所示的方式放置,点A1、A2、A3…和B1、B2、B3…分别在直线y=kx+b和x轴上,如果A1(1,-1),A2($\frac{7}{2}$,$\frac{3}{2}$),则点A2016的坐标是(5×($\frac{3}{2}$)2015-4,($\frac{3}{2}$)2015).