题目内容
7.①解方程组$\left\{\begin{array}{l}{2x-y=-8}\\{5x+3y=2}\end{array}\right.$②求不等式组$\left\{\begin{array}{l}{2x+5≤3(x+2)}\\{x-1<\frac{x}{3}}\end{array}\right.$的解集,并写出它的整数解.
分析 (1)根据方程组的解法解答即可;
(2)根据不等式组的解法解答即可.
解答 解:(1)$\left\{\begin{array}{l}{2x-y=-8①}\\{5x+3y=2②}\end{array}\right.$,
①×3+②得:x=-2,
把x=-2代入①得:y=4,
所以方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+5≤3(x+2)①}\\{x-1<\frac{x}{3}②}\end{array}\right.$,
解不等式①得:x≥-1,
解不等式②得:x<1.5,
所以不等式组的解集为:-1≤x<1.5,
所以它的整数解为:-1,0,1.
点评 此题考查不等式组的解集,关键是根据方程组和不等式组的解法解答.

练习册系列答案
相关题目
2.为了求1+2+22+23+…+22016的值,可令S=1+2+22+23+…+22016,则2S=2+22+23+24+…+22017,因此2S-S=22017-1,所以1+2+22+23+…+22016=22017-1.仿照以上推理计算出1+3+32+33+…+32016的值是( )
| A. | 32017-1 | B. | 32018-1 | C. | $\frac{{3}^{2017}-1}{4}$ | D. | $\frac{{3}^{2017}-1}{2}$ |
16.下列结论正确的是( )
| A. | x2-2是二次二项式 | |
| B. | 单项式-x2的系数是1 | |
| C. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-2 | |
| D. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 |

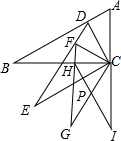 如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.
如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.