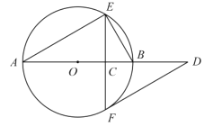
题目内容
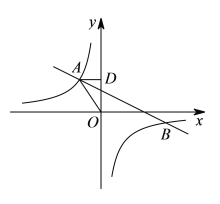
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
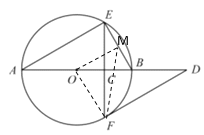
(1)已知![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
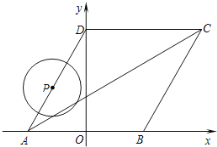
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,请补全图形;若
,请补全图形;若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)![]() =
=![]() ;(2)
;(2)![]() 的半径为4.
的半径为4.
【解析】
(1)连接OF,求出∠BOF=2∠A=![]() ,利用DF是
,利用DF是![]() 的切线证得∠CFD=∠COF=
的切线证得∠CFD=∠COF=![]() 即可得到答案;
即可得到答案;
(2)如图,连接OM,根据M是BE的中点,O是AB的中点求出∠MOB=![]() ,∠OMB=90°,设
,∠OMB=90°,设![]() 的半径为r得到OM=
的半径为r得到OM=![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,求出r即可.
,求出r即可.
(1)连接OF,
∵![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,
,
∴![]() ,∠ACE=∠ACF=90°,
,∠ACE=∠ACF=90°,
∴∠BOF=2∠A=![]() ,∠OFC+∠COF=90°,
,∠OFC+∠COF=90°,
∵DF是![]() 的切线,
的切线,
∴∠OFD=90°,
∴∠OFC+∠CFD=90°,
∴∠CFD=∠COF=![]() ,
,
即![]() =
=![]() ;
;

(2)如图,连接OM,
∵M是BE的中点,O是AB的中点,
∴OM∥AE,
∠MOB=![]() ,∠OMB=90°,
,∠OMB=90°,
设![]() 的半径为r,
的半径为r,
∴OM=![]() ,
,
∵∠BOF=2∠A=60°,
∴∠MOF=90°,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得r=4,
∴![]() 的半径为4.
的半径为4.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目