Question

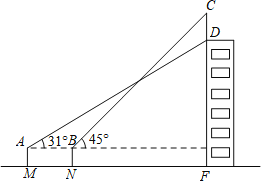
【题目】如图是一种简易台灯的结构图，灯座为△ABC，A、C、D在同一直线上，量得∠ACB=90°，∠A=60°，AB=16cm，∠ADE=135°，灯杆CD长为40cm，灯管DE长为15cm.求台灯的高(即台灯最高点E到底盘AB的距离).(结果取整，参考数据sin15°≈0.26，cos15°≈0.97，tan15°≈0.27，≈1.73)

Answer 1

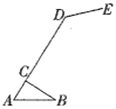
【答案】台灯的高约为45cm.

【解析】

如图，作DG⊥AB，EF⊥AB，交AB延长线于G、F，DH⊥EF于H，可得四边形DGFH是矩形，可得DG=FH，根据∠A的余弦可求出AC的长，进而可得AD的长，根据∠A的正弦即可求出DG的长，由∠ADE=135°可得∠EDH=15°，根据∠DEH的正弦可得EH的长，根据EF=EH+FH求出EF的长即可得答案.

如图，作DG⊥AB，EF⊥AB，交AB延长线于G、F，DH⊥EF于H，

∴四边形DGFH是矩形，

∴DG=FH，

∵∠A=60°，AB=16，

∴AC=AB·cos60°=16×=8，

∴AD=AC+CD=8+40=48，

∴DG=AD·sin60°=24，

∵DH⊥EF，AF⊥EF，

∴DH//AF，

∴∠ADH=180°-∠A=120°，

∵∠ADE=135°，

∴∠EDH=∠ADE-∠ADH=15°，

∵DE=15，

∴EH=DE·sin15°≈3.9，

∴EF=EH+FH=EH+DG=24+3.9≈45，

答：台灯的高约为45cm.