题目内容
15．用适当方法解下列方程（1）x2-3x-10=0；
（2）2（x+1）2=18；
（3）x2+2x-2024=0；
（4）2x2+3x=4．
分析 （1）利用因式分解法解方程；
（2）利用直接开平方法解方程；
（3）利用配方法解方程；
（4）利用公式法解方程．
解答 解：（1）（x-7）（x+3）=0，
x-7=0或x+3=0，
x-7=0或x+3=0，
所以x1=7，x2=-3；
（2）（x+1）2=9，
x+1=±3，
所以x1=-4，x2=2；
（3）x2+2x+1=2025，
（x+1）2=2025，
x+1=±45，
所以x1=-46，x2=44；
（4）2x2+3x-4=0，
△=32-4×2×（-4）=41，
x=$\frac{-3±\sqrt{41}}{2×2}$，
所以x1=$\frac{-3+\sqrt{41}}{4}$，x2=$\frac{-3-\sqrt{41}}{4}$．
点评 本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了公式法解一元二次方程．
练习册系列答案
相关题目
7．当x=-2011时，计算下列各式的值．
（1）$\frac{x-|x|}{2}$×$\frac{x+|x|}{2}$；
（2）$\frac{-x+|x|}{2}$÷$\frac{x-|x|}{2}$．
（1）$\frac{x-|x|}{2}$×$\frac{x+|x|}{2}$；
（2）$\frac{-x+|x|}{2}$÷$\frac{x-|x|}{2}$．
6．
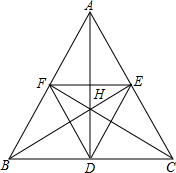如图，锐角△ABC的垂心为H，三条高的垂足分为D、E、F，则H是△DEF的（ ）
如图，锐角△ABC的垂心为H，三条高的垂足分为D、E、F，则H是△DEF的（ ）| A． | 垂心 | B． | 重心 | C． | 内心 | D． | 外心 |
如图，?ABCD中，AE平分∠DAB，∠B=100°，则∠DAE等于40°．