题目内容
5.已知a、b、c满足(a-12)2+$\sqrt{b-5}$+|c-13|=0.(1)求a、b、c的值;
(2)以a、b、c为三边能否构成直角三角形?说明理由.
分析 (1)根据非负数的性质可得a-12=0,b-5=0,c-13=0,进而可得答案;
(2)根据勾股定逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形可得答案.
解答 解:(1)∵(a-12)2+$\sqrt{b-5}$+|c-13|=0,
∴a-12=0,b-5=0,c-13=0,
解得:a=12,b=5,c=13;
(2)能.∵122+52=132,
∴a2+b2=c2,
∴能构成直角三角形.
点评 此题主要考查了非负数的性质,以及勾股定逆定理,关键是掌握绝对值、偶次幂、算术平方根都具有非负性.

练习册系列答案
相关题目
16.方程(x-5)(7-2x)=x-5的根是( )
| A. | 5和3 | B. | 3 | C. | -3 | D. | -5和-3 |
20. 如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带( )
如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带( )
 如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带( )
如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带( )| A. | 带①去 | B. | 带②去 | C. | 带③去 | D. | 带①②去 |
17.九边形的对角线有( )
| A. | 25条 | B. | 31条 | C. | 27条 | D. | 30条 |
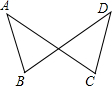 已知:如图,AB=DC,AC=BD.
已知:如图,AB=DC,AC=BD.