题目内容
14.如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以1cm/s和3cm/s的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.(1)如图1,设点P运动时间为ts,当点P在AC上,点Q 在BC上时,
①用含t的式子表示CP和CQ,则CP=t,CQ=3t;
②若△PEC≌△CFQ,则CP的对应边是QC;
③结合①②,当t=1 s时,△PEC≌△CFQ;
(2)请问:除了(1)这种情况,△PEC与△QFC有没有可能全等?若能,求出运动时间;若不能,请说明理由.
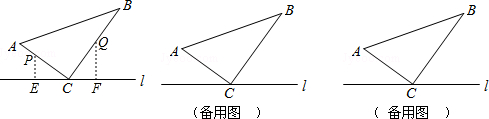
分析 (1)①根据路程=速度×时间,即可解答;
②若△PEC与△QFC全等,则CP的对应边是QC,
③由△PEC与△QFC全等,得到PC=QC.可得6-t=8-3t,即可解答;
(2)除了(1)这种情况,△PEC与△QFC有可能全等,①当点P与点Q重合,△PEC与△QFC全等,然后计算出t的值即可.②当点Q到点A时,停止,点P运动到BC上时,t-6=6即可得出结论.
解答 解:(1)①根据路程=速度×时间可得:CP=t,CQ=3t,故答案为:t,3t;
②若△PEC与△QFC全等,则CP的对应边是QC,
故答案为:QC.
③∵△PEC与△QFC全等,
∴PC=QC.
∴6-t=8-3t.
解得:t=1.
故答案为:1.
(2)如图2所示: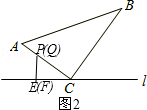
∵点P与点Q重合,
∴△PEC与△QFC全等,
∴6-t=3t-8.
解得:t=3.5.
当点P在BC上,点Q到点A时,t-6=6,
∴t=12,
即:满足条件的时间为3.5或12秒.
点评 本题考查了全等三角形的性质定理与判定定理,解决本题的关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
4.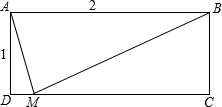 矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
 矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{4}$ | C. | $\sqrt{3}-\frac{3}{2}$ | D. | $2-\sqrt{3}$ |
2.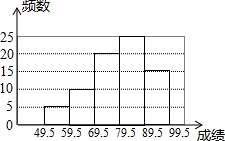 某校八年级(2)班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全部人数的( )
某校八年级(2)班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全部人数的( )
 某校八年级(2)班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全部人数的( )
某校八年级(2)班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全部人数的( )| A. | 20% | B. | 25% | C. | 30% | D. | 35% |
3.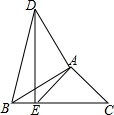 如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
 如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
4.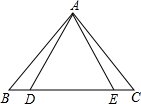 如图,已知△ABE≌△ACD,下列不正确的等式是( )
如图,已知△ABE≌△ACD,下列不正确的等式是( )
 如图,已知△ABE≌△ACD,下列不正确的等式是( )
如图,已知△ABE≌△ACD,下列不正确的等式是( )| A. | AB=AC | B. | ∠BAE=∠CAD | C. | BE=DC | D. | AD=DE |
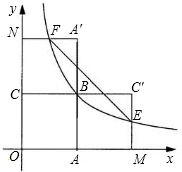 如图,四边形OABC是面积为4的正方形,函数$y=\frac{k}{x}$(x>0)的图象经过点B.
如图,四边形OABC是面积为4的正方形,函数$y=\frac{k}{x}$(x>0)的图象经过点B.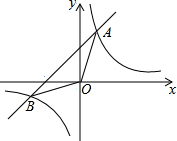 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交反比例函数y=$\frac{k}{x}$的图象于另一点B.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的直线y=x+b交反比例函数y=$\frac{k}{x}$的图象于另一点B.