题目内容
16.已知|a-1|+(ab-2)2=0,求$\frac{1}{(a+2)(b+2)}$+$\frac{1}{(a+3)(b+3)}$+$\frac{1}{(a+4)(b+4)}$+…+$\frac{1}{(a+2011)(b+2011)}$+$\frac{1}{(a+2012)(b+2012)}$值.分析 根据非负数的性质列式求出a、b的值,然后将所求代数式裂项并整理,再代入进行计算即可得解.
解答 解:由题意得,a-1=0,ab-2=0,
解得a=1,b=2,
所以,原式=$\frac{1}{3×4}$+$\frac{1}{4×5}$+$\frac{1}{5×6}$+…+$\frac{1}{2012×2013}$+$\frac{1}{2013×2014}$,
=$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{6}$+…+$\frac{1}{2012}$-$\frac{1}{2013}$+$\frac{1}{2013}$-$\frac{1}{2014}$,
=$\frac{1}{3}$-$\frac{1}{2014}$,
=$\frac{2011}{6042}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0,本题难点在于将所求代数式裂项.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
16.如果向西走5m,记作+5m,那么-15m表示( )
| A. | 向东走15m | B. | 向南走15m | C. | 向西走15m | D. | 向北走15m |
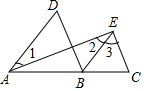 如图,已知A、B、C三点在同一直线上,∠1=∠2,∠D=∠3.
如图,已知A、B、C三点在同一直线上,∠1=∠2,∠D=∠3.