题目内容
8.已知动点P以2cm/秒的速度沿图甲的边框按B→C→D→E→F→A的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=6cm,试回答下列问题: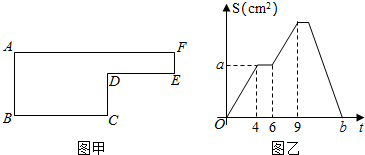
(1)图甲中的BC长是8cm,图乙中的a=24,b=17.
(2)图甲中的图形面积是多少?
分析 (1)根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度可得BC的长;又由AB=6cm,可以计算出△ABP的面积,计算可得a的值;计算BC+CD+DE+EF+FA的长度,又由P的速度,计算可得b的值.
(2)分析图形可得,甲中的图形面积等于AB×AF-CD×DE,根据图象求出CD和DE的长,代入数据计算可得答案.
解答 解:(1)动点P在BC上运动时,对应的时间为0到4秒,易得:BC=2cm/秒×4秒=8cm;
a=$\frac{1}{2}$×BC×AB=24cm2.
根据题意,动点P共运动了BC+CD+DE+EF+FA=8+4+6+2+14=34cm,
其速度是2cm/秒,则b=$\frac{34}{2}$=17秒;
故答案为:8cm;24;17;
(2)由图可得:CD=2×2=4cm,DE=2×3=6cm,
则AF=BC+DE=14cm,
又由AB=6cm,
则甲图的面积为AB×AF-CD×DE=60cm2,
答:图甲中的图形面积的60cm2.
点评 本题考查动点问题的函数图象,解题的关键是读懂图意,明确横轴与纵轴的意义.

练习册系列答案
相关题目
19.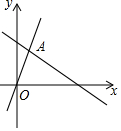 如图,函数y=2x和y=ax+4的图象相交于点A (m,3),则不等式2x<ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A (m,3),则不等式2x<ax+4的解集为( )
 如图,函数y=2x和y=ax+4的图象相交于点A (m,3),则不等式2x<ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A (m,3),则不等式2x<ax+4的解集为( )| A. | $x<\frac{3}{2}$ | B. | $x>\frac{3}{2}$ | C. | x<3 | D. | x>3 |
16.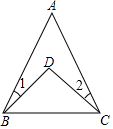 如图,∠1=15°,∠2=20°,∠A=40°,则∠BDC的度数为( )
如图,∠1=15°,∠2=20°,∠A=40°,则∠BDC的度数为( )
 如图,∠1=15°,∠2=20°,∠A=40°,则∠BDC的度数为( )
如图,∠1=15°,∠2=20°,∠A=40°,则∠BDC的度数为( )| A. | 75° | B. | 95° | C. | 105° | D. | 115° |
13.对整式3x2-12y2因式分解正确的是( )
| A. | 3(x2-4y2) | B. | 3(x+2y)(x-2y) | C. | 3(2x+y)(2x-y) | D. | 3(x-2y)2 |
20.某地区植树造林2009年达到2万公顷,预计从2010年开始,以后每年比前一年多植树2万公顷(2010年为第一年),则年植树面积y(万亩)与年数x(年)的关系是( )
| A. | y=2+0.5x | B. | y=2+x | C. | y=2+2x | D. | y=2x |
 如图,抛物线y=-$\frac{1}{4}$x2+$\frac{9}{4}$与直线y=-$\frac{1}{2}$x+$\frac{3}{2}$交于点A,C的两点,点B是点A关于y轴的对称点.
如图,抛物线y=-$\frac{1}{4}$x2+$\frac{9}{4}$与直线y=-$\frac{1}{2}$x+$\frac{3}{2}$交于点A,C的两点,点B是点A关于y轴的对称点.