题目内容
17. 如图,抛物线y=-$\frac{1}{4}$x2+$\frac{9}{4}$与直线y=-$\frac{1}{2}$x+$\frac{3}{2}$交于点A,C的两点,点B是点A关于y轴的对称点.
如图,抛物线y=-$\frac{1}{4}$x2+$\frac{9}{4}$与直线y=-$\frac{1}{2}$x+$\frac{3}{2}$交于点A,C的两点,点B是点A关于y轴的对称点.(1)求A,B,C两点的坐标.
(2)当点P在x轴上运动时,若以A,B,C,P为顶点的四边形是平行四边形,求P点的坐标.
(3)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
(4)将(3)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在请说明理由.
分析 (1)将y=-$\frac{1}{4}$x2+$\frac{9}{4}$与y=-$\frac{1}{2}$x+$\frac{3}{2}$组成方程组可求得方程组的解,从而得到点A和点C的坐标,然后关于y轴对称点的坐标特点可求得点B的坐标;
(2)先求得AB的长,然后依据平行四边形对边相等的性质可得到PC=2,故此可得到点P的坐标;
(3)①当点F在第一象限时,设点F的坐标为F(p,p),将点F的坐标代入y=-$\frac{1}{2}$x+$\frac{3}{2}$上,可求得P的值,从而得到点F的坐标;②当点F在第二象限时,同理可得点F的坐标为(-3,3),此时点F不在线段AC上舍去;
(4)过点M作MH⊥DN于H,依据题意可知OD=t,由(3)可知正方形GDCF的边长为1则OE=t+1,然后用含t式子表示出点N(t,-$\frac{1}{2}$t+$\frac{3}{2}$),点M(t+1,-$\frac{1}{2}$t+1),从而可得到DN、DM、MN的长,然后分为DN=DM、ND=NM、MN=MD三种情况列方程求解即可.
解答 解:(1)∵抛物线y=-$\frac{1}{4}$x2+$\frac{9}{4}$与直线y=-$\frac{1}{2}$x+$\frac{3}{2}$交于点A,C的两点,
∴-$\frac{1}{4}$x2+$\frac{9}{4}$=-$\frac{1}{2}$x+$\frac{3}{2}$,整理得:x2-2x-3=0,解得:x=-1或x=3.
将x=-1代入y=-$\frac{1}{2}$x+$\frac{3}{2}$得:y=2,
∴点A的坐标为(-1,2).
∵点B是点A关于y轴的对称点,
∴点B的坐标为(1,2).
将x=3代入y=-$\frac{1}{2}$x+$\frac{3}{2}$得:y=0,
∴点C的坐标为(3,0).
(2)∵点A的坐标为(-1,2),点B的坐标为(1,2),
∴AB=2.
∵以A,B,C,P为顶点的四边形是平行四边形,
∴PC=AB=2.
又∵C的坐标为(3,0),点P在x轴上,
∴C的坐标为(1,0)或(5,0);
(3)①当点F在第一象限时,如图1所示: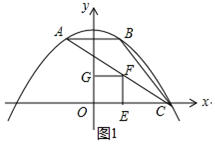
设正方形OEFG的边长为P,则F(p,p).
∵点F(p,p)在直线y=-$\frac{1}{2}$x+$\frac{3}{2}$上,
∴-$\frac{1}{2}$p+$\frac{3}{2}$=p,解得p=1,
∴点F的坐标为(1,1).
②当点F在第二象限时,同理可得点F的坐标为(-3,3),此时点F不在线段AC上,舍去.
综上所述:点F的坐标为(1,1);
(4)过点M作MH⊥DN于H,如图2,则OD=t,OE=t+1.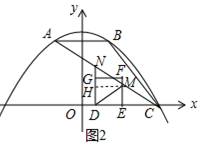
∵点E和点C重合时停止运动,
∴0≤t≤2.
当x=t时,y=-$\frac{1}{2}$t+$\frac{3}{2}$,则N(t,-$\frac{1}{2}$t+$\frac{3}{2}$),DN=-$\frac{1}{2}$t+$\frac{3}{2}$,
当x=t+1时,y=-$\frac{1}{2}$(t+1)+$\frac{3}{2}$=-$\frac{1}{2}$t+1,则M(t+1,-$\frac{1}{2}$t+1),ME=-$\frac{1}{2}$t+1,
在Rt△DEM中,DM2=12+(-$\frac{1}{2}$t+1)2=$\frac{1}{4}$t2-t+2.
在Rt△NHM中,MH=1,NH=(-$\frac{1}{2}$t+$\frac{3}{2}$)-(-$\frac{1}{2}$t+1)=$\frac{1}{2}$,
∴MN2=12+($\frac{1}{2}$)2=$\frac{5}{4}$.
①当DN=DM时,(-$\frac{1}{2}$t+$\frac{3}{2}$)2=$\frac{1}{4}$t2-t+2,解得t=$\frac{1}{2}$;
②当ND=NM时,-$\frac{1}{2}$t+$\frac{3}{2}$=$\frac{\sqrt{5}}{2}$,解得t=3-$\sqrt{5}$;
③当MN=MD时,$\frac{5}{4}$=$\frac{1}{4}$t2-t+2,解得t1=1,t2=3(舍去).
综上所述:当△DMN是等腰三角形时,t的值为$\frac{1}{2}$,3-$\sqrt{5}$或1.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了用方程组求函数交点的坐标、平行四边形的性质、等腰三角形的定义,用含t的式子表示出△MND的三边长是解题的关键.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案| A. | 3 | B. | 0 | C. | $-\frac{1}{4}$ | D. | 4 |
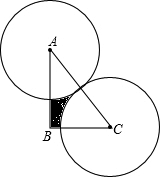 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,分别以A、C为圆心,以$\frac{AC}{2}$的长为半径作圆,将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为6-$\frac{25}{16}$πcm2(结果保留π)
如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,分别以A、C为圆心,以$\frac{AC}{2}$的长为半径作圆,将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为6-$\frac{25}{16}$πcm2(结果保留π) 如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,过点C作CE⊥AB于点E,如果AD=3,BD=8,那么△ADC的周长为19.
如图,△ABC中,∠A=80°,∠B=40°,BC的垂直平分线交AB于点D,连结DC,过点C作CE⊥AB于点E,如果AD=3,BD=8,那么△ADC的周长为19.