��Ŀ����
����Ŀ���Ķ����в��ϣ�
����չʾ��
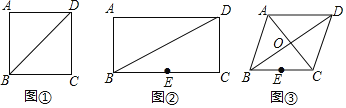
����һ����ͼ![]() ����
����![]() �У��ص���������ABC�Ķ���
�У��ص���������ABC�Ķ���![]() ��ƽ����
��ƽ����![]() �۵�������B���C�غϣ����
�۵�������B���C�غϣ����![]() ��
��![]() �ġ��ýǡ�����ͼ
�ġ��ýǡ�����ͼ![]() ����
����![]() ������
�У�����![]() ��ƽ����
��ƽ����![]() �۵��������ظ����֣��ٽ����²�����
�۵��������ظ����֣��ٽ����²�����![]() ��ƽ����
��ƽ����![]() �۵�������
�۵�������![]() ���C�غϣ����
���C�غϣ����![]() ��
��![]() �ġ��ýǡ���
�ġ��ýǡ���
���ζ�����ͼ![]() ����
����![]() ������
�У�����![]() ��ƽ����
��ƽ����![]() �۵��������ظ����֣��ٽ����²�����
�۵��������ظ����֣��ٽ����²�����![]() ��ƽ����
��ƽ����![]() �۵��������ظ�����
�۵��������ظ�����![]() �ظ��۵�n�Σ���������
�ظ��۵�n�Σ���������![]() ���C�غϣ����
���C�غϣ����![]() ��
��![]() �ġ��ýǡ���̽�����֣�
�ġ��ýǡ���̽�����֣�![]() ������
������![]()
![]() ��ͼ
��ͼ![]() ����
����![]() ��
��![]() �ġ��ýǡ�����
�ġ��ýǡ�����![]() ��
��![]() ��������ϵ�ǣ�______��
��������ϵ�ǣ�______��
![]() ��ͼ
��ͼ![]() ����
����![]() ��
��![]() �ġ��ýǡ�����
�ġ��ýǡ�����![]() ��
��![]() ��������ϵ�ǣ�______��
��������ϵ�ǣ�______��
![]() ��ͼ
��ͼ![]() ����
����![]() ��
��![]() �ġ��ýǡ�����
�ġ��ýǡ�����![]() ��
��![]() ��������ϵ�ǣ�______��
��������ϵ�ǣ�______��
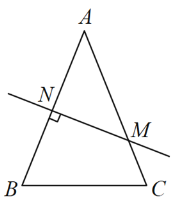
Ӧ��������
![]() ���һ�������ε������Ƿֱ�Ϊ
���һ�������ε������Ƿֱ�Ϊ![]() ��
��![]() ��
��![]() �����Ƿ���
�����Ƿ���![]() ��
��![]() �������Ƕ��Ǵ������εġ��ýǡ��������һ�������Σ����������Ǿ��Ǵ������εġ��ýǡ�������֪��С�Ľ���
�������Ƕ��Ǵ������εġ��ýǡ��������һ�������Σ����������Ǿ��Ǵ������εġ��ýǡ�������֪��С�Ľ���![]() �������������ǵĶ�����
�������������ǵĶ�����



���𰸡���1��![]() �� ��2��
�� ��2��![]() �� ��3��
�� ��3��![]() ��
��
��4���������ε����������ǵĶ����ֱ�Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() .
.
��������
��1���ɸ��������֪��![]() ��
��![]() �غϣ���
�غϣ���![]() ��
��
��2�����������![]() ��
��![]() ����Ϊ
����Ϊ![]() ������
������![]() ��
��
��3������������ۿ�֪����![]() �����ý������۵��Ĵ������ǡ�BΪ��C�ı�������
�����ý������۵��Ĵ������ǡ�BΪ��C�ı�������![]() ��
��
��4���������֪�������ε����������Ƕ���12�㱶��������������Ƿֱ�Ϊ![]() ��
��![]() �����������ε��ڽǺͶ�����������m��n��ֵ����.
�����������ε��ڽǺͶ�����������m��n��ֵ����.
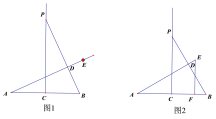
![]() ��ͼ1�У�
��ͼ1�У�![]() ��
��![]() �����ý�����
�����ý�����
![]() ��
��![]() �غϣ�
�غϣ�
![]() ��
��
�ʴ�Ϊ![]() ��
��
![]() ��ͼ2�У�
��ͼ2�У�![]() ��
��![]() ��ƽ����
��ƽ����![]() �۵���
�۵���
![]() ��
��
��![]() �����²�����
�����²�����![]() ��ƽ����A1B2�۵�����ʱ��
��ƽ����A1B2�۵�����ʱ��![]() ���C�غϣ�
���C�غϣ�
![]() ��
��
![]() ��Ƕ���
��Ƕ���![]() ��
��
![]() ��
��
�ʴ�Ϊ��![]() ��
��
![]() ����������ۿ�֪��
����������ۿ�֪��
��1���۵�ʱ��![]() �����ý���������
�����ý���������![]() ��
��
��2���۵�ʱ��![]() �����ý���������
�����ý���������![]() ��
��
��3���۵�ʱ��![]() �����ý���������
�����ý���������![]() ��
��
![]()
��n���۵�ʱ��![]() �����ý���������
�����ý���������![]() ��
��
�ʴ�Ϊ![]() ��
��
![]() ��Ϊ��С����
��Ϊ��С����![]() ��
��![]() �ĺýǣ�
�ĺýǣ�
���ݺýǶ��壬����������Ƿֱ�Ϊ![]() ��
��![]() ����m��n����������
����m��n����������![]() ��
��
�����⣬��![]() ��
��
��![]() ��
��
��m��n����������������m��![]() ��14���������ӣ�
��14���������ӣ�
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��������ε����������ǵĶ����ֱ�Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() .
.

 �������ϵ�д�
�������ϵ�д�