题目内容
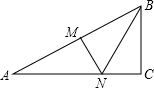 如图,Rt△ABC中,∠ACB=90°,BC=3,AC=3
如图,Rt△ABC中,∠ACB=90°,BC=3,AC=3| 3 |
| A、0 | B、1 | C、2 | D、3 |
考点:线段垂直平分线的性质
专题:
分析:解直角三角形求出∠A=30°,根据线段垂直平分线上的点到两端点的距离相等可得AN=BN,再根据等边对等角可得∠ABN=∠A,再根据直角三角形两锐角互余求出∠CBN=30°,从而得解.
解答:解:∵tan∠A=
=
=
,
∴∠A=30°,
∵MN是AB的中垂线,
∴AN=BN,
∴∠ABN=∠A=30°,
∵∠ACB=90°,
∴∠CBN=90°-30°-30°=30°,
∴等于30°的角是∠A、∠ABN、∠CBN共3个.
故选D.
| BC |
| AC |
| 3 | ||
3
|
| ||
| 3 |
∴∠A=30°,
∵MN是AB的中垂线,
∴AN=BN,
∴∠ABN=∠A=30°,
∵∠ACB=90°,
∴∠CBN=90°-30°-30°=30°,
∴等于30°的角是∠A、∠ABN、∠CBN共3个.
故选D.
点评:本题考查了线段垂直平分线上的点到两端点的距离相等的性质,等边对等角的性质,直角三角形两锐角互余的性质,解直角三角形,熟记各性质是解题的关键.

练习册系列答案
相关题目
 如图是泰安市某一天内的气温变化图,下列结论中错误的是( )
如图是泰安市某一天内的气温变化图,下列结论中错误的是( )| A、这一天中最高气温是24℃ |
| B、这一天中最高气温与最低气温的差为16℃ |
| C、这一天中2时至14时之间的气温在逐渐升高 |
| D、这一天中气温在逐渐降低的只有14时至24时 |
下列说法中错误的是( )
| A、过直线外一点有且只有一条直线平行于已知直线 |
| B、两条直线平行,同旁内角互补 |
| C、在同一平面内不相交的两条直线叫做平行线 |
| D、有公共顶点,有一条公共边且互补的两个角叫邻补角 |
某个事件发生的概率是
,这意味着( )
| 1 |
| 2 |
| A、在两次重复试验中该事件必有一次发生 |
| B、在一次试验中没有发生,下次肯定发生 |
| C、在一次事件中已经发生,下次肯定不发生 |
| D、每次试验中事件发生的可能性是50% |
二次根式
可化简成( )
| (-2)2 |
| A、-2 | ||
| B、4 | ||
| C、2 | ||
D、
|
 如图,一条公路修到湖边时,需拐弯绕湖而过,第一次拐的角∠A=110°,第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的度数为( )
如图,一条公路修到湖边时,需拐弯绕湖而过,第一次拐的角∠A=110°,第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的度数为( )| A、120° | B、130° |
| C、140° | D、150° |
 如图,D为△ABC的AB边的中点,过点D作AB的垂线交BC于点E,连接AE,若AC=8cm,BC=12cm,则△ACE的周长为( )
如图,D为△ABC的AB边的中点,过点D作AB的垂线交BC于点E,连接AE,若AC=8cm,BC=12cm,则△ACE的周长为( )| A、20cm | B、18cm |
| C、15cm | D、12cm |
 完成推理填空:
完成推理填空: