Question

如图，在平面直角坐标系中，一次函数y=kx+2（k≠0）的图象与反比例函数y=

m

x

(m≠0)的图象在第一象限内交于点A（3，n），与x轴交于点B，与y轴交于点C，tan∠CBO=

2

3

．
（1）求一次函数和反比例函数的解析式；
（2）若在x轴上存在点P，使得AB=BP，求点P的坐标．

Answer 1

考点：反比例函数综合题

专题：

分析：（1）首先求出C点坐标，进而得出BO的长，求出k的值，再利用tan∠ABD=

AD

BD

，得出AD的长，进而得出反比例函数解析式；
（2）首先得出AB的长，进而得出BP的长，求出a的值即可．

解答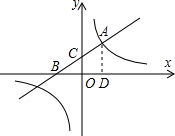：解；（1）在直线y=kx+2上，令x=0，则y=2，
∴C点坐标为；（0，2），
在Rt△BCO中，
tan∠CBO=

CO

BO

，
∴

2

3

=

2

BO

，
∴BO=3，
∴B点坐标为：（-3，0），
∵直线y=kx+2经过点B，
∴-3k+2=0，
解得：k=

2

3

，
∴一次函数为：y=

2

3

x+2，
过点A作AD⊥x轴于点D，
∵A为（3，n），
∴OD=3，
∴BD=BO+OD=6，
在Rt△ABD中，
tan∠ABD=

AD

BD

，
∴

2

3

=

AD

6

，
解得；AD=4，
∴A点坐标为；（3，4），
∵y=

m

x

经过点A，
∴m=12，
∴反比例函数为；y=

12

x

；

（2）在Rt△ABD中，
AB=

BD2+AD2

=2

13

，
设P为（a，0），
∴BP=|a+3|=2

13

，
∴a=2

13

-3或a=-2

13

-3，
∴P点坐标为：（2

13

-3，0）或（-2

13

-3，0）．

点评：此题主要考查了反比例函数综合以及一次函数的性质，根据数形结合得出m的值是解题关键．