题目内容
已知?ABCD中,∠A=40°,则下列判断正确的是( )
| A、∠B=140°,∠C=140° |
| B、∠C=140°,∠D=140° |
| C、∠B=140°,∠D=140° |
| D、∠B=40°,∠D=140° |
考点:平行四边形的性质
专题:
分析:根据平行四边形的性质和平行线的性质求解即可.
解答:解:在?ABCD中,
∵∠A=40°,AD∥BC,
∴∠B=180°-∠A=140°,∠C=40°,∠D=∠B=140°,
故选C.
∵∠A=40°,AD∥BC,
∴∠B=180°-∠A=140°,∠C=40°,∠D=∠B=140°,
故选C.
点评:本题考查了平行四边形的性质和平行线的性质,解答本题的关键是掌握平行四边形对角相等的性质.

练习册系列答案
相关题目
方程ax2+bx+c=0的两个根是x1,x2,则ax2+bx+c分解因式的结果是( )
| A、ax2+bx+c=(x-x1)(x-x2) |
| B、ax2+bx+c=(ax-x1)(ax-x2) |
| C、ax2+bx+c=a(x+x1)(x+x2) |
| D、ax2+bx+c=a(x-x1)(x-x2) |
若以a=5,b=12,c=13作为一个三角形的三边,那么以5n,12n,13n(n>0)作为一个三角形的三边,这个三角形的形状是( )
| A、直角三角形 |
| B、等腰三角形 |
| C、钝角三角形 |
| D、等腰直角三角形 |
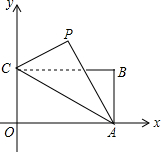 如图,在平面直角坐标系中,矩形OABC的长OA=
如图,在平面直角坐标系中,矩形OABC的长OA= 如图,在平面直角坐标系中,一次函数y=kx+2(k≠0)的图象与反比例函数
如图,在平面直角坐标系中,一次函数y=kx+2(k≠0)的图象与反比例函数 通过计算图中所示的几何图形的面积,可表示的代数恒等式是
通过计算图中所示的几何图形的面积,可表示的代数恒等式是