题目内容
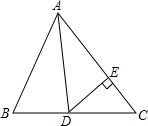 在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.(1)求∠ADB,∠ADC的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据三角形内角和定理可求∠BAC的度数,根据角平分线的定义可求∠BAD,∠DAC,再根据三角形的内角和得出∠ADB,利用邻补角得出∠ADC;
(2)根据高线的定义和三角形内角和定理即可求解.
(2)根据高线的定义和三角形内角和定理即可求解.
解答:解:(1)∵在△ABC中,∠B=66°,∠C=54°,
∴∠BAC=60°,
∵AD是△ABC角平分线,
∴∠BAD=∠DAC=
∠BAC=30°,
∴∠ADB=180°-∠B-∠BAD=84°,
∴∠ADC=96°;
(2)∵DE是△ADC的高线,
∴∠DEA=90°,
∴∠ADE=60°.
∴∠BAC=60°,
∵AD是△ABC角平分线,
∴∠BAD=∠DAC=
| 1 |
| 2 |
∴∠ADB=180°-∠B-∠BAD=84°,
∴∠ADC=96°;
(2)∵DE是△ADC的高线,
∴∠DEA=90°,
∴∠ADE=60°.
点评:考查了角平分线的定义,高线的定义和三角形内角和定理:三角形内角和等于180°.

练习册系列答案
相关题目
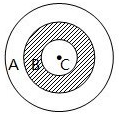 如图,有三个同心圆,由里向外的半径依次是2cm,4cm,6cm将圆盘分为三部分,飞镖可以落在A.B.C任何一部分内,则下列说法正确的是( )
如图,有三个同心圆,由里向外的半径依次是2cm,4cm,6cm将圆盘分为三部分,飞镖可以落在A.B.C任何一部分内,则下列说法正确的是( )A、飞镖在A区域可能性为
| ||
B、飞镖在B区域可能性为
| ||
C、飞镖在C区域可能性为
| ||
D、飞镖在三个区域可能性都为
|
 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA+sinB=
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA+sinB=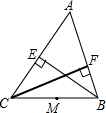 如图,BE、CF是△ABC的高,M为BC的中点.试说明点B、C、E、F在以点M为圆心的同一圆上.
如图,BE、CF是△ABC的高,M为BC的中点.试说明点B、C、E、F在以点M为圆心的同一圆上.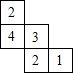 一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和从左面看到的这个几何体的形状图.