题目内容
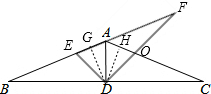
 如图,已知等腰△ABC,AD是底边BC上的高,AD:DC=1:3,将△ADC绕着点D旋转,得△DEF,点A、C分别与点E、F对应,且EF与直线AB重合,设AC与DF相交于点O,则S△AOF:S△DOC=
如图,已知等腰△ABC,AD是底边BC上的高,AD:DC=1:3,将△ADC绕着点D旋转,得△DEF,点A、C分别与点E、F对应,且EF与直线AB重合,设AC与DF相交于点O,则S△AOF:S△DOC=考点:旋转的性质
专题:
分析:如图,作DG⊥AB于G,设AD=x,则BD=3x,由勾股定理就可以求出AB=
x,由三角形的面积公式求出DG的值,由三角函数值求出AG,就可以表示出AE,从而求出AF,再由△AFO∽△DCO就可以求出结论.
| 10 |
解答:解:作DG⊥AB于G,
∵AB=AC,AD⊥BC,
∴∠ADB=∠ADC=90°,∠BAD=∠CAD,∠B=∠C.
设AD=x,则BD=3x,由勾股定理,得
AB=
x,
∴AC=
x.
∴
=
,
∴
=
,
∴GD=
.
∵
=
=tan∠C.
∴tan∠B=
.
∵∠ADG+∠GAD=90°,∠B+∠GAD=90°,
∴∠ADG=∠B.
∴tan∠ADG=
=
,
∴
=
,
∴AG=
.
∵△FDE是由△CDA旋转得来的,
∴△FDE≌△CDA,
∴DE=DA.∠F=∠C.
∵DG⊥AB,
∴AG=EG.
∴AE=2AG,
∴AE=
.
∴AF=
x-
=
.
∵∠AOF=∠DOC,∠F=∠C,
∴△AFO∽△DCO,
∴S△AOF:S△DOC=(
)2=(
)2.
=
.
故答案为:
.
∵AB=AC,AD⊥BC,
∴∠ADB=∠ADC=90°,∠BAD=∠CAD,∠B=∠C.
设AD=x,则BD=3x,由勾股定理,得
AB=
| 10 |
∴AC=
| 10 |
∴
| AD•BD |
| 2 |
| AB•GD |
| 2 |
∴
| x•3x |
| 2 |
| ||
| 2 |
∴GD=
3
| ||
| 10 |
∵
| AD |
| DC |
| 1 |
| 3 |
∴tan∠B=
| 1 |
| 3 |

∵∠ADG+∠GAD=90°,∠B+∠GAD=90°,
∴∠ADG=∠B.
∴tan∠ADG=
| AG |
| GD |
| 1 |
| 3 |
∴
| AG | ||||
|
| 1 |
| 3 |
∴AG=
| ||
| 10 |
∵△FDE是由△CDA旋转得来的,
∴△FDE≌△CDA,
∴DE=DA.∠F=∠C.
∵DG⊥AB,
∴AG=EG.
∴AE=2AG,
∴AE=
| ||
| 5 |
∴AF=
| 10 |
| ||
| 5 |
4
| ||
| 5 |
∵∠AOF=∠DOC,∠F=∠C,
∴△AFO∽△DCO,
∴S△AOF:S△DOC=(
| AF |
| DC |
| ||||
| 3x |
=
| 32 |
| 45 |
故答案为:
| 32 |
| 45 |
点评:本题考查了等腰三角形的性质的运用,勾股定理的运用,旋转的性质的运用,三角函数值的运用,相似三角形的判定与性质的运用,三角形面积公式的运用,解答时证明三角形相似是关键.

练习册系列答案
相关题目
关于近似数1.6万,下列说法正确的是( )
| A、精确到十分位 |
| B、精确到万位 |
| C、精确到个位 |
| D、精确到千位 |
若x<y成立,则下列不等式成立的是( )
| A、4x<3y | ||||
| B、-x<-y | ||||
C、
| ||||
| D、x+6<y+6 |
 如图,已知在扇形OAB中,∠AOB=90°,半径OA=10,正方形FCDE的四个顶点分别在
如图,已知在扇形OAB中,∠AOB=90°,半径OA=10,正方形FCDE的四个顶点分别在