题目内容
6．
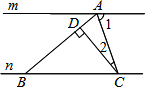如图，直线m∥n，点A在直线m上，点B，C在直线n上，AB=BC，∠1=70°，CD⊥AB于D，那么∠2等于（ ）| A． | 20° | B． | 30° | C． | 32° | D． | 25° |
分析 先由平行线的性质得出∠ACB=∠1=70°，根据等角对等边得出∠BAC=∠ACB=70°，由垂直的定义得到∠ADC=90°，那么∠2=90°-∠DAC=20°．
解答 解：∵m∥n，
∴∠ACB=∠1=70°，
∵AB=BC，
∴∠BAC=∠ACB=70°，
∵CD⊥AB于D，
∴∠ADC=90°，
∴∠2=90°-∠DAC=90°-70°=20°．
故选A．
点评 本题考查了平行线的性质，等腰三角形的判定，垂直的定义，三角形内角和定理，求出∠BAC=70°是解题的关键．
练习册系列答案
相关题目
17．若顺次连结四边形ABCD各边中点所得四边形是矩形，则原四边形必定是（ ）
| A． | 正方形 | B． | 对角线相等的四边形 | ||
| C． | 菱形 | D． | 对角线相互垂直的四边形 |
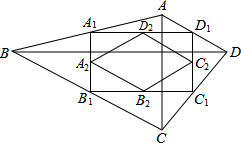如图，四边形ABCD中，AC=a，BD=b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2，如此进行下去，得到四边形AnBnCnDn．