题目内容
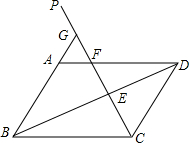如图：过?ABCD的顶点C作射线CP分别交BD、AD于E、F，交BA的延长线于G
（1）求证：CE2=EF•EG；
（2）若GF=3，CE=2，求EF的长．
（1）证明：∵AB∥CD，
∴
=
，
∵AD∥BC，
∴=
，
∴=，
∴CE2=EF•EG；
（2）解：∵CE2=EF•EG，GF=3，CE=2，
∴22=EF（3+EF），
整理得出：EF2+3EF-4=0，
解得：EF=1或-4（不合题意舍去）．
故EF的长为1．
分析：（1）利用平行线分线段成比例定理以及比例的性质求出=，=，即可得出=，得出答案即可；
（2）利用（1）中所求得出关于EF的一元二次方程求出即可．
点评：此题主要考查了平行线分线段成比例定理以及一元二次方程的解法，利用平行线分线段成比例定理得出=是解题关键．
∴
=，∵AD∥BC，
∴
=，∴
=，∴CE2=EF•EG；
（2）解：∵CE2=EF•EG，GF=3，CE=2，
∴22=EF（3+EF），
整理得出：EF2+3EF-4=0，
解得：EF=1或-4（不合题意舍去）．
故EF的长为1．
分析：（1）利用平行线分线段成比例定理以及比例的性质求出
=，=，即可得出=，得出答案即可；（2）利用（1）中所求得出关于EF的一元二次方程求出即可．
点评：此题主要考查了平行线分线段成比例定理以及一元二次方程的解法，利用平行线分线段成比例定理得出
=是解题关键． 
练习册系列答案
相关题目
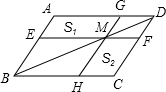（2012•包头）如图，过?ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH，那么图中的?AEMG的面积S1与?HCFM的面积S2的大小关系是（ ）
如图，过?ABCD的中心O作OE⊥BD，交AD于点E，∠DBC=20°，则∠EBD=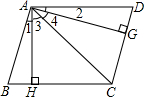
如图，过?ABCD的顶点A分别作AH⊥BC于点H、AG⊥CD于点G，且AH≠AG，AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4，则下列关系正确的是（ ）
如图：过?ABCD的顶点C作射线CP分别交BD、AD于E、F，交BA的延长线于G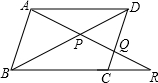
如图，过?ABCD的顶点A的直线交BD于点P，交CD于点Q，交BC的延长线于点R．