题目内容
如图，过?ABCD的中心O作OE⊥BD，交AD于点E，∠DBC=20°，则∠EBD=20°
20°
．分析：由过?ABCD的中心O作OE⊥BD，可得EO是BD的垂直平分线，即可得BE=DE，又由等边对等角，即可得∠EBD=∠EDB，又由∠DBC=20°，利用平行线的性质，即可求得答案．
解答：解：∵点O是?ABCD的中心，
∴OB=OD，
∵OE⊥BD，
∴BE=DE，
∴∠EBD=∠EDB，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠EDB=∠DBC=20°，
∴∠EBD=20°．
故答案为：20°．
∴OB=OD，
∵OE⊥BD，
∴BE=DE，
∴∠EBD=∠EDB，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠EDB=∠DBC=20°，
∴∠EBD=20°．
故答案为：20°．
点评：此题考查了平行四边形的性质、线段垂直平分线的性质以及等腰三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
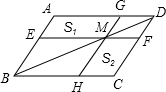（2012•包头）如图，过?ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH，那么图中的?AEMG的面积S1与?HCFM的面积S2的大小关系是（ ）
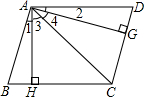如图，过?ABCD的顶点A分别作AH⊥BC于点H、AG⊥CD于点G，且AH≠AG，AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4，则下列关系正确的是（ ）
如图：过?ABCD的顶点C作射线CP分别交BD、AD于E、F，交BA的延长线于G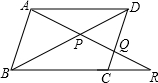
如图，过?ABCD的顶点A的直线交BD于点P，交CD于点Q，交BC的延长线于点R．